Yapay Zeka Kışı ve Kaybolan Gradyan Problemi
Bugün her ne kadar yapay zeka alanında inanılmaz ilerleyişler olsa da yapay zeka bugünlerine gelirken birden çok kez kışa saplandı ve uzun yıllar buradan çıkamadı. Bu yazıda özellikle son dönemki yapay zeka kışından çıkışı sağlayıp bize güneşli günleri göstermiş gelişmelerden sonra anladığımız kaybolan gradyan problemine bir bakışta nelerin sebep olduğunu ve nasıl aşıldığına değineceğiz.
Nöral ağların ilkel formu olan basit algılayıcılar XOR kapısı gibi non-lineer problemler ile başa çıkamamaktaydı. Bunun sebebi aktivasyon fonksiyonu olarak kullanılan basamak fonksiyonunun türevi olmayan bir fonksiyon olmasıydı. İlk yapay zeka kışı ile karşılaşmamız bu problemin fark edilmesi ile olmuştu.

Algılayıcı dizaynında çoklu katman kullanımının birinci yapay zeka kışının sonunu getireceğini 16 yıl sonra 1986 yılında anlamıştık. Fakat bu sadece birinci yapay zeka kışının geçmesini sağlamıştı!

Bu buluş dizayn değişikliği ile birlikte kullanılan aktivasyon fonksiyonunun türevi alınabilen bir fonksiyon ile değişimini de gerektirmişti. Bu şekilde hataları geriye doğru yayabiliyor (geri yayılım algoritması – backpropagation) ve öğrenimi sağlayabiliyorduk. Ortaya atılması o günlere rastlayan lojistik sigmoid ve hiperbolik tanjant (tanh) fonksiyonları uzun yıllar popülerliğini sürdürecekti. Fakat bu fonksiyonların beraberinde büyük aksaklıklar getirdiğini anlamamız yıllarımızı alacaktı!
İkinci yapay zeka kışı

Sigmoid fonksiyonu -5 ve +5 girdileri arasında anlamlı sonuçlar üretmektedir. Fonksiyonun türevi bu aralıkta 0’dan farklıdır. Bu demek oluyor ki bu aralıktaki girdiler için türev alınabildiğinden hataları geriye doğru yayabilir ve öğrenimi sürdürebiliriz.
GAN’ın mucidi yapay zekanın altın çocuğu Ian Goodfellow, doktora tezinde bu anlamlı aralığı Bart Simpson’un kaykayı ile bu fonksiyon üzerinde hareket edebilmesi ile resmetmiştir. Yer çekimi Bart’ın [-5, +5] aralığında hareket etmesini sağlayacaktır.


Genil ve derin ağlar her katmanda büyük çıktılar üretilmesine neden olmaktadır. Sigmoid aktivasyon fonksiyonu kullanılarak dizayn edilmiş derin bir ağ gradyanın kaybolması ya da patlaması problemini doğuracaktır. Bu da bizi yeniden bir yapay zeka kışına sokmuş olacaktır.

Güneşli günler
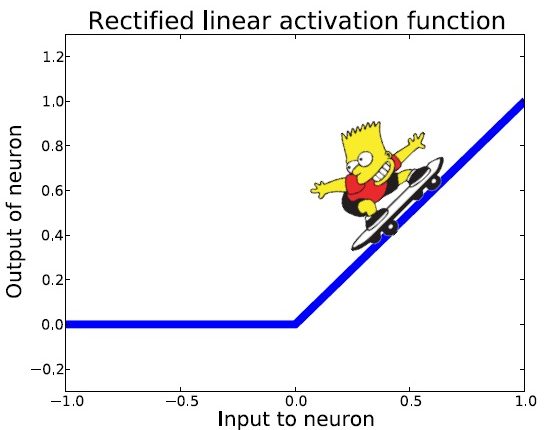
İkinci yapay zeka kışından çıkılması 2011 yılına rastlamaktadır. ReLU olarak adlandırılan çok basit bir aktivasyon fonksiyonunun ortaya atılması baharı getirmiştir. Bu fonksiyon pozitif girdiler için birim ya da özdeşlik fonksiyonu iken negatif girdiler için sıfır sonucunu üretmektedir.

Bart’ın kaykayı ile yapacağı hareketleri bu yeni fonksiyon üzerinde hayal edelim. Her pozitif girdi için Bart hareket edebilecektir.

Derin ağların da çoğunlukla katmanlar boyunca büyük pozitif çıktılar ürettiğini göz önüne alırsak bu yeni fonksiyon ile büyükçe bir problemimiz çözülmüş olacaktır. Yine de bazı katmanlar büyük negatif çıktılar üretirse türev alınamayacak ve öğrenim gerçekleşemeyecektir.

Bu noktada sızıntılı ReLU (Leaky ReLU) aktivasyon fonksiyonu her derdinize derman olabilir. Pozitif bölgelerde daha hızlı olmak kaydı fonksiyonun (sıfır noktası haricinde) her noktasında türevi alınabilmekte bu da Bart’ın herhangibir noktada hareket edebilmesini sağlamaktadır.

Test
Geniş ve derin bir nöral ağ inşa edelim. Basitçe el yazısıyla yazılmış rakamların sınıflandırılması için bir model kuracağız. Çok derin olmayacak olsa da sırasıyla 128, 64, 32 ve 16 düğümden oluşan 4 gizli katmanlı bir modelimiz olsun. Aktivasyon fonksiyonu olarak da sigmoid’i seçtik.
|
1 2 3 4 5 6 7 8 9 10 11 |
classifier = tf.contrib.learn.DNNClassifier( feature_columns=feature_columns , n_classes=10 #0 to 9 - 10 classes , hidden_units=[128, 64, 32, 16] , optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.1) , activation_fn = tf.nn.sigmoid ) |
Model görüldüğü üzere bir hayal kırıklığı yaratmakta. Başarı oldukça düşük.

Şimdi de sadece aktivasyon fonksiyonunu ReLU ile değiştirelim.
|
1 2 3 4 5 6 7 8 9 10 11 |
classifier = tf.contrib.learn.DNNClassifier( feature_columns=feature_columns , n_classes=10 #0 to 9 - 10 classes , hidden_units=[128, 64, 32, 16] , optimizer=tf.train.GradientDescentOptimizer(learning_rate=0.1) , activation_fn = tf.nn.relu ) |
Sadece aktivasyon fonksiyonunu değiştirerek başarının dramatik olarak yükseldiğini görüyoruz.

Bu yazı sırasında geliştirilmiş uygulamaya ait kaynak kodu GitHub‘ta bulabilirsiniz.
Yapay zeka çalışmaları aktivasyon fonksiyonları sebebiyle 1986 ve 2006 yılları arasında çokça üretken olmayan bir dönem geçirdi. Komik olsa da bu kadar zor bir problem çokça basit bir fonksiyonun kullanımı ile çözülebildi. ReLU ve türevleri bugün yapay zeka alanındaki neredeyse çoğu ilerlemenin nedenidir.
Bu yazı, An Overview to Gradient Vanishing Problem yazısından Türkçe’ye çevrilmiştir.