Javascript: Ne Ola ki bu “Zaman Karmaşıklığı ve Büyük-O Notasyonu” dedikleri şeyler?

By Tahir Kardak On Şub 16, 2021

Yazıma ekşi sözlükte bir arkadaşın yazdığı bir şiirle başlamak istiyorum.

Ayni input, ayni runtime
Bir tat alamiyorum
Allah’im bu nasil complexity
Hesaplayamıyorum.

Son dönemlerde ismini sıkça duymaya başladığımız kavramlardan iki tanesi olan Zaman Karmaşıklığından (Time complexity) ve Büyük-O nostasyonu (Big-O notation) bahsetmek istiyorum. Aslında bu kavramlar yeni kavramlar değil. 1894 yılında ilk olarak Paul Gustav tarafından ortaya atılmış ve Bilgisayar mühendisliğinde Algoritma Analizi derslerinde anlatılmaktadır.

Peki son dönemlerde neden önem kazandı bu kavramlar? Bulut teknolojilerinde (Amazon, Azure) kullanılan her ram, cpu vb. başına ödeme yapılması, cep telefonları, giyilebilir teknolojiler, küçük donanımlı teknolojilerin(raspberry pi, arduino vb) kaynaklarının küçük olması ve bu sistemlerin aşırı yüklenmelere karşı güçlü olmaması gibi durumlardan dolayı önem kazanmaya başlamıştır. Yani çalışan bir uygulama geliştirme dönemi sona eriyor. Minimum kaynaklarla maksimumum performans elde etme dönemi yükselişe geçiyor. Bu yükselişle birlikte bu yöntemler önem kazanıyor. Alaylı yazılımcıların uygulama geliştirirken çoğu zaman göz ardı ettiği kavramlardır.

Bir algoritmanın verimliliği; CPU kullanım, bellek , disk , Ağ(network ) kaynakların kullanımı gibi durumlara da bağlıdır. Konumuz Zaman karmaşıklığı ve büyük-o notasyonu olduğu için bu kaynakların kullanımından bahsetmeyeceğim.

Bu kadar uzun girizgahtan sonra bu iki kavramın tanımı ile başlayalım.

ZAMAN KARMAŞIKLIĞI (TIME COMPLEXITY)

Bir algoritmanın çalıştırılması için geçen süreyi tanımlar. Buradaki süre, zaman olarak değil algoritmanın tamamlanması için yapılan işlem sayısının hesaplanmasıdır.Bu kavramı uygulamanın performansı olarak ta düşünebiliriz.



let dizi = [1,4,54,34,57,87,93,23,45,67];

function degerVarmi(x){ 
    for (i = 0; i < dizi.length; i++) {
       if (dizi[i] == x)
         return true;
       else 
         return false;
   }
}

console.log(degerVarmi(1)); // best-case
console.log(degerVarmi(87)); // average-case
console.log(degerVarmi(67)); // worst-case
console.log(degerVarmi(100)); // worst-case

let dizi = [1,4,54,34,57,87,93,23,45,67];

function degerVarmi(x){

for (i = 0; i < dizi.length; i++) {

if (dizi[i] == x)

return true;

else

return false;

}

console.log(degerVarmi(1)); // best-case

console.log(degerVarmi(87)); // average-case

console.log(degerVarmi(67)); // worst-case

console.log(degerVarmi(100)); // worst-case

Yukarıdaki örnek için zaman karmaşıklığını hesaplayalım:

Dizi tanımlama işlemi için 1 işlem (3.satır). DegerVarmi fonksiyonun içinde döngü işlemi yapılıyor(üç ile onuncu satır) ve dizinin boyutu kadar işlem yapılacaktır. Dizinin boyu 10 işlem olduğundan burada 10 işlem gerçekleşecektir. Dizin içerisindeki işlem sayısı ise şu şekildedir. Karşılaştırma işlemi 1 işlem. true değerinin dönme işlemi 1 işlem, else için 1 işlemi false değerinin dönmesi için 1 işlem. Fonksiyonun tamamında 4*10 = 40 işlem yapılacaktır

Fonksiyonun çağrılması ve ekrana yazılması 2 işlem (14.satır). Aynı işlem dört kere yapıldığı için buradaki işlem sayısı 8‘dir (13 ile 17. satır)

Yukarıdaki algoritmanın karmaşıklığı 4*n+12;

Algoritmayı aşağıdaki şekilde yaparsak zaman karmaşıklığı n+9 olacaktır. yani n olacaktır.



let dizi = [1,4,54,34,57,87,93,23,45,67];

function degerVarmi(x){ 
    for (i = 0; i < dizi.length; i++) {
       return dizi[i] == x;
   }
}

console.log(degerVarmi(1)); // best-case
console.log(degerVarmi(87)); // average-case
console.log(degerVarmi(67)); // worst-case
console.log(degerVarmi(100)); // worst-case

let dizi = [1,4,54,34,57,87,93,23,45,67];

function degerVarmi(x){

for (i = 0; i < dizi.length; i++) {

return dizi[i] == x;

}

console.log(degerVarmi(1)); // best-case

console.log(degerVarmi(87)); // average-case

console.log(degerVarmi(67)); // worst-case

console.log(degerVarmi(100)); // worst-case

Ama her iki örneğin zaman karmaşıklığı linear karmaşıklığa sahip olacaktır yani O(N)’dir.

Yukarıdaki örnekte O(N) kavramından bahsettik . Buradan Büyük-O Nostasyonunun tanımına geçiş yapalım.

Büyük-O Notasyonu (Big-O Notation)

Yazılan algoritmanın, girdi sayısı büyüdükçe, oluşacak karmaşıklığının artış hızını göstermek için kullanılan araçlardan birisidir.

Büyük-O Notasyonu, algoritma için zaman karmaşıklığı için en kötü duruma göre üst sınırı verir. Girdi sayısı keyfi olarak büyüdükçe algoritmanın performansının ölçülmesinde yardımcı olur.

Girdi sayısına göre artış hızı küçük olan algoritma tercih edilir. Bir algoritma için, eğer girdi sayının artış hızına göre, zaman karmaşıklığı da hızla artıyorsa varsa diğer alternatif algoritmalar düşünülmeli.

Küçük veriler setlerinde bu durum çok sorun teşkil etmese de, veri sayısının çok olduğu sistemlerde büyük sorunlar ortaya çıkabilir.

Büyük-O terimleri ve Senaryoları

Konuyu daha iyi anlamak için bazı aşağıdaki kavramlardan bahsetmek gerekiyor. Yazının devamındaki aşağıdaki kavramlara örnekler verilecektir.

Terimler (Tercih edilme sırasına göre)

O(1): Constant(Sabit)
O(NlogN) : Linearithmic
O(N): Linear
O(logN): Logarithmic(logaritmik)
O (N²): Quadratic(İkinci dereceden)
O (N³): Cubic (Üçüncü dereceden)
O(c^N): Exponential(Üstel), c sabit değer.
O(N!) : Factorial(Faktoriyel)

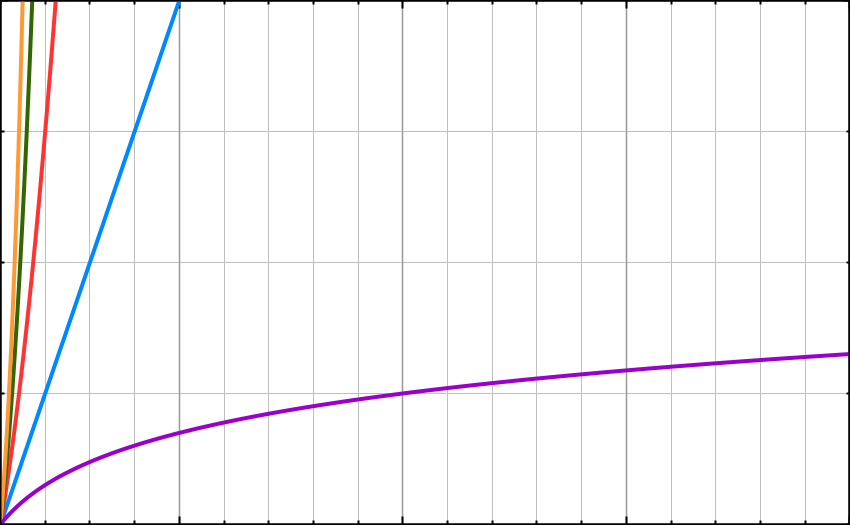
Veri setine göre algoritmanın Büyük-O sınıflandırması aşağıdaki grafikten görülebilir.

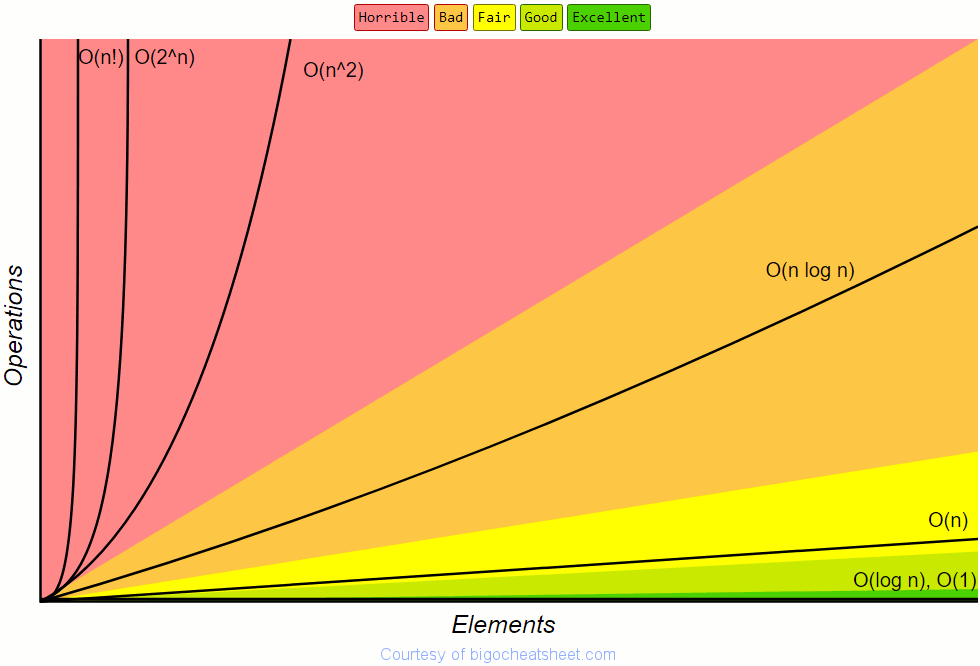
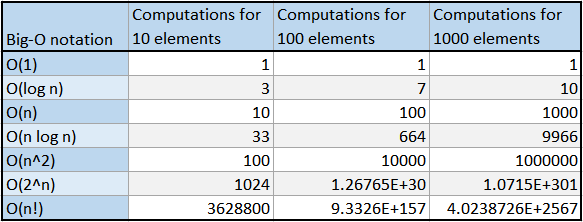
Veri setine göre Büyük-O karşılaştırması aşağıdaki tabloda gösterilmiştir.

Know Thy Complexities!

Hi there! This webpage covers the space and time Big-O complexities of common algorithms used in Computer Science. When…

www.bigocheatsheet.com

Senaryolar

Konuyu daha iyi anlamak için bir dizi içerisinde bir elemanı aramayı düşünelim. Örnek olarak; dizimiz [1,4,6,5,3,9,8] şeklinde olsun. (İlk örneğimizde yorum kısmında ingilizce yazan bölümleri dikkat ettiniz mi?)

Best-case: Aranılan değerin 1 olması durumunu ele alalım. İlk iterasyonda bu değer bulunacağı için bu en iyi durumdur.
Average-case: Aranılan değerin 5 olması durumunu ele alalım. 5 değeri 4. iterasyonda bulunacağı için bu ortalama durumdur. Veri setinin dağılımına göre bu durum değişebilir.
Worst-case: Aranılan değerin 8 olması durumunu ele alalım. Tüm dizi taranacağı için bu en kötü senaryodur. Diğer bir kötü senaryo için de aranılan değer 2 olsun. Bu durumda tüm diziyi taranacak ve 2 değer bulunmayacaktır.

Dizilerin küçükten büyüğe doğru sıralaması içinde düşünülebilir(Bubble sort) Karşılaşılabilecek senaryolar şu şekildedir. Verilen dizinin sıralı olması en iyi senaryodur. Verilen dizinin büyükten küçüğe doğru sıralanmış olması durumu ise en kötü senaryodur.

O(1): Constant(Sabit)

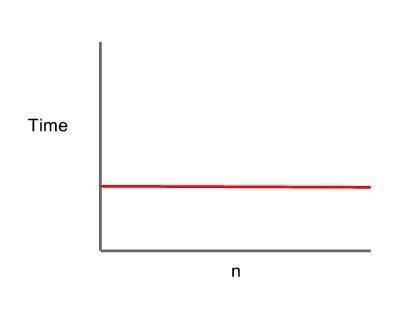
Algoritmanın çalışma zamanın girdi değerine bağlı olmaması durumdur. Veri seti ne kadar büyük olursa olsun çalışma süresi ve kaynak kullanımı değişmez hep aynı kalır. Değişken tanımla, değişkene değer atama, fonksiyona parametre geçme, konsola bir değer yazdırma, yeni bir dizi tanımlama, dizinin ilk ve son elemanların alınması, dizin bir elemanına yeni değer atanması vb işlemlerin Big-O değeri O(1)’dır

Aşağıdaki tüm işlemler 0(1) karmaşıklığına sahiptir.



let a;
a =1;
let dizi = [1,2,3,4];
let x = dizi[0];
let y = dizi.length;
let z = dizi[y-1];
dizi[2] =10;
console.log(dizi);
dizi.pop();
dizi.push(5);
z > y;

function ciftMi(sayi) {
  return sayi % 2 ==0;
}
ciftMi(5);

let a;

a =1;

let dizi = [1,2,3,4];

let x = dizi[0];

let y = dizi.length;

let z = dizi[y-1];

dizi[2] =10;

console.log(dizi);

dizi.pop();

dizi.push(5);

z > y;

function ciftMi(sayi) {

return sayi % 2 ==0;

}

ciftMi(5);

Grafik olarak gösterimi ise şu şekildedir:

O(N): Linear

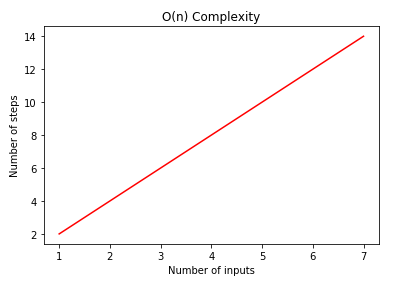
Çalışma süresi, girdinin büyüklüğüne doğrudan bağımlı olan algoritmadır. Girdi sayısı büyüdükçe çalışma süresi de benzer şekilde büyür. Gerçek hayattan örnek verecek olursak; Yorulma payı göz ardı edildiğinde 1 km 13 dakikada yürünürse , 2 km 26 dakikada yürünür, 5 km 65 dk’da yürünür. Dizlerde elaman arama, dizinin en büyük veya en küçük değerini bulma algoritmaları, döngü işlemleri Linear karmaşıklığa sahiptir.



let dizi = [6,54,34,57,87,93,23,4,45,67];

function enKucukDegerBul(){
  let enKucukDeger = dizi[0];
  for (var i=0; i<dizi.length; i++){
    if (dizi[i]<enKucukDeger){
        enKucukDeger = dizi[i];
    }
  }
  return enKucukDeger;
}

console.log(enKucukDegerBul());

let dizi = [6,54,34,57,87,93,23,4,45,67];

function enKucukDegerBul(){

let enKucukDeger = dizi[0];

for (var i=0; i<dizi.length; i++){

if (dizi[i]<enKucukDeger){

enKucukDeger = dizi[i];

}

return enKucukDeger;

}

console.log(enKucukDegerBul());

Yukarıdaki örnekte 7. satırda bir döngü işlemi gerçekleşiyor. Dizinin eleman sayısı kadar işlem yapılacaktır. Döngünün içinde bir işlem olduğu için (dizinin eleman sayısı X 1) olacaktır. Yani O(N) karmaşıklığı olacaktır.

Linear Karmaşıklığın grafiksel gösterimi şu şekildedir.

O (N²): Quadratic (İkinci derece)

Algoritmaya verilen girdi boyutunun karesi ile doğru orantılı olduğu durumdur. Örneğin bir dizinin boyutu 10 ise 10*10 şeklinde işlem gerçekleşir. Bu durum genellikle iç içe iki döngünün oluğu veya dizilerde sıralama işleminin yapıldığı algoritmalarda ortaya çıkar.

Büyük-O notasyonunda işlem sayısı ile ilgileniyoruz, işlemin sonucu ile ilgilenmiyoruz.



let dizi = [6,54,34,57,87,93,23,4,45,67];

function degerleriCarp(){
  for(let i =0; i<dizi.length; i++){
    for(let j=0; j<dizi.length; j++){
      console.log(`deger:  ${dizi[i] * dizi[j]}`);
    }
  }
}

degerleriCarp();

let dizi = [6,54,34,57,87,93,23,4,45,67];

function degerleriCarp(){

for(let i =0; i<dizi.length; i++){

for(let j=0; j<dizi.length; j++){

console.log(`deger: ${dizi[i] * dizi[j]}`);

}

degerleriCarp();

Yukarıdaki örnekte dizinin her bir elemanını yine kendisi ile çarparak ekrana yazdırıyoruz. Sabit değerleri dışarıda bırakarak işlem sayısı dizinin eleman sayısının kendisi ile çarpımıdır. Sonuç olarak bu algoritmanın Büyük-O karmaşıklığı O (N²)’dır.

Quadratic Karmaşıklığın grafiksel gösterimi şu şekildedir.

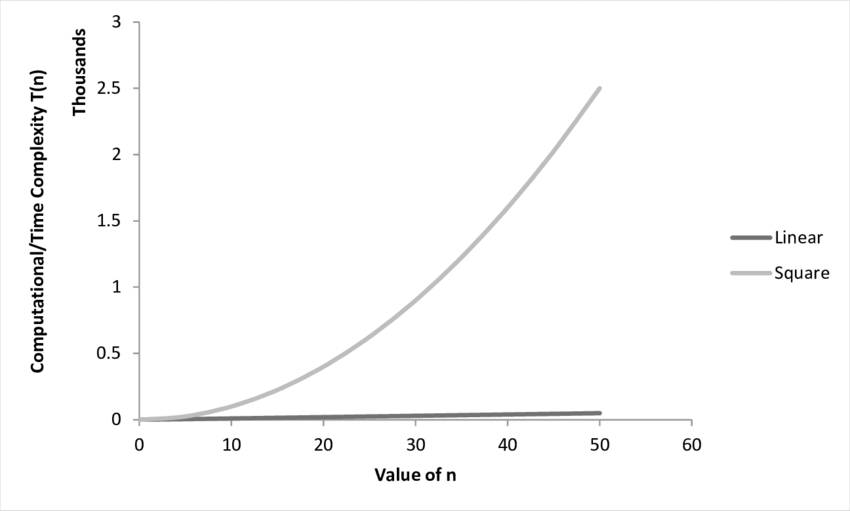
Dizilerin sıralama işlemlerinde bu durumun ortaya çıkacağını söylemiştik. Bubble Sort algoritmasının karmaşıklığını bulalım.

Bubble Sort

Sıralanacak dizinin üzerinde sürekli ilerlerken her defasında iki elemanın birbiriyle karşılaştırılıp, karşılaştırılan elemanların yanlış sırada olmaları durumunda yerlerinin değiştirilmesi mantığına dayanır. Sıralama işlemi tamamlanana kadar algoritma dizinin başına dönerek kendisini yineler. Aşağıdaki videoda algoritmanın çalışma mantığını görebilirsiniz.



function bubbleSort(array) {
  let length = array.length;
  for (let i = 0; i < length; i++) {
    for (let j = 0; j < (length - i - 1); j++) {
      if (array[j] > array[j + 1]) {
        let tmp = array[j];
        array[j] = array[j + 1];
        array[j + 1] = tmp;
      }
    }
  }
  return array;
}
 console.log(bubbleSort( [1,54,34,57,87,93,23,45,4,67]));

function bubbleSort(array) {

let length = array.length;

for (let i = 0; i < length; i++) {

for (let j = 0; j < (length - i - 1); j++) {

if (array[j] > array[j + 1]) {

let tmp = array[j];

array[j] = array[j + 1];

array[j + 1] = tmp;

}

return array;

}

console.log(bubbleSort( [1,54,34,57,87,93,23,45,4,67]));

Yukarıdaki örnekte aynı dizi üzerinde 2 kere döngü işlemi yapılmaktadır. Algoritmanın Büyük-O karmaşıklığı O (N²)’dır. Girdi sayısı arttıkça çalışma süresi de artacaktır.

O(N³), O(N⁴): Yapmayın böyle şeyler

İç içe iki döngü O (N²) karmaşıklığını veriyorsa 3 döngü O(N³), 4 döngü ile O(N⁴) karmaşıklığını verecektir. Girdi sayısının çok büyük olduğu durumlarda algoritmanın süresi çok çok daha uzun sürede bitecektir.



let dizi = [6,54,34,57,87,93,23,4,45,67];

function carpmaIslemi(){
  for (let i = 0; i < dizi.length; i++){
    for (let j = 0; j < dizi.length; j++){
      for (let k = 0; k < dizi.length; k++){
        console.log(dizi[i]*dizi[j]*dizi[k]);
    }
  }
}
}
  
carpmaIslemi();

let dizi = [6,54,34,57,87,93,23,4,45,67];

function carpmaIslemi(){

for (let i = 0; i < dizi.length; i++){

for (let j = 0; j < dizi.length; j++){

for (let k = 0; k < dizi.length; k++){

console.log(dizi[i]*dizi[j]*dizi[k]);

}

carpmaIslemi();

Yukarıdaki örnekte 3 tane döngü işlemi var ve dizinin elaman sayısı 10 olduğunda 10*10*10 = 1000 kere işlem yapılacaktır. Eğer bir döngü daha eklerse 10*10*10*10 = 10000 kere işlem yapılacaktır.

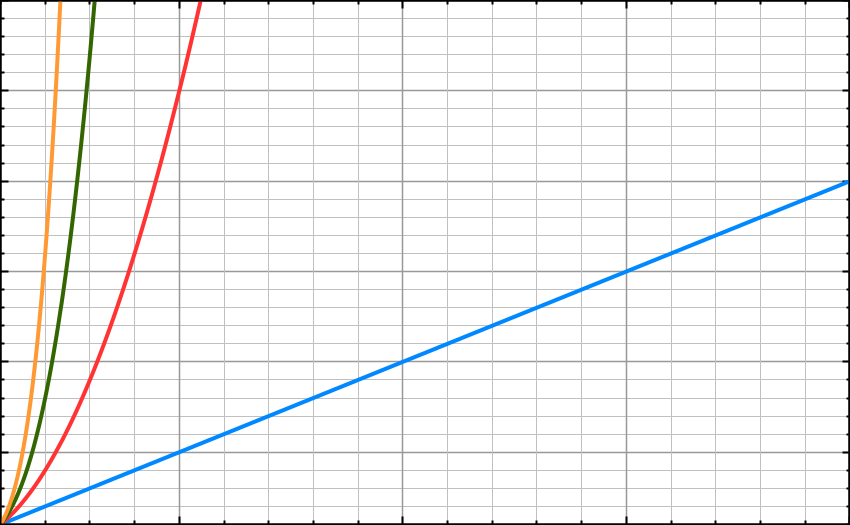
LOGARİTMİK KARMAŞIKLIKLAR

Logaritmik karmaşıklıklara geçemeden önce logaritmanın kısa bir tanımını yapmak istiyorum.

Matematikte toplamanın tersi, çıkarma işlemi ise üs(bir sayıyı kendisi ile çarpma )işleminin tersi de logaritmadır.

Kafanız karıştı ise Wikipedia’daki tanımını aşağıya yazıp zaman karmaşıklığı konumuza dönmek istiyorum.

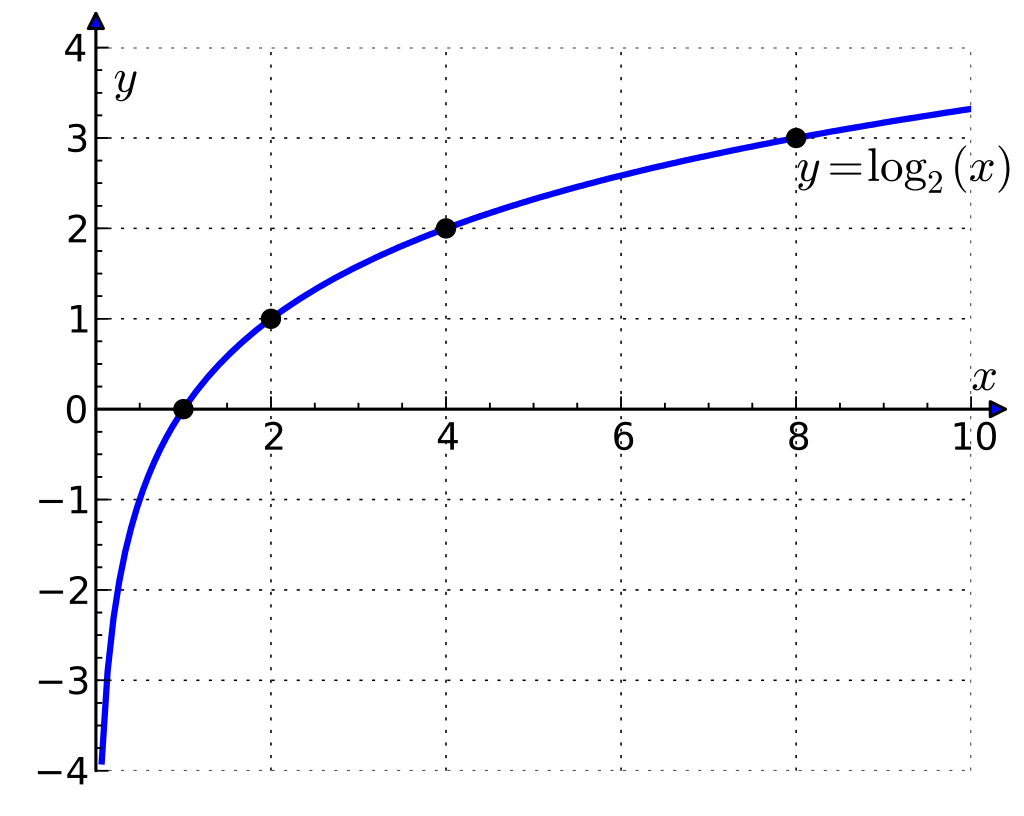
Logaritma, üstel işlevlerin tersinin hesaplanmasına duyulan ihtiyaç sonucu ortaya çıkmıştır. Örneğin 2’nin küpü 8’dir. Burada 3’ü ifade etmek için logaritmaya ihtiyaç vardır. log2( 8) = 3. — Wikipedia

Logaritmik karmaşıklıklar genellikle var olan sorun için veri setini her seferinde ikiye bölen algoritmalarda kullanılır.

Gerçek hayattan örnek verecek olursak. Elimizde var olan 1024 sayfalık telefon rehberinden bir numarayı aradığımızı düşünelim. İşlemi rehberin tam ortasından(512. sayfa) başlayıp aradığımız numara 512’den önceki sayfalarda ise arama işlemine bu aralıkta devam edilir, değilse 512’den büyük olan diğer aralıktan devam edilir. Aradığımız numara 512. sayfadan önce olsun. Bu sefer 512. sayfasının yarısı olan 256. sayfayı açıp aradığımız numara 256’dan önceki sayfada mı diye kontrol ederiz. Bu şekilde hedeflenen numarayı bulmak için bölmeye devam ederiz. Numarayı en fazla 10 işlemde bulabiliriz. Eğer 1. sayfadan aramaya başlayıp sayfaları tek tek kontrol etseydik en fazla 1024 işlem yapmamız gerekecekti. Yukarıda anlattığım durumu kanlı canlı görmek isterseniz, şu videoyu izleyebilirsiniz.

O(logN) — Binary Search

Yukarıdaki örneğimizdeki arama işleminin yapıldığı algoritmadır. Bu işlemin yapılması için veri setinin sıralanmış olması gerekiyor. Aksi durumda bu algoritma çalışmayacaktır. Aşağıdaki görselde bu algoritmanın çalışma mantığı gösterilmiştir.

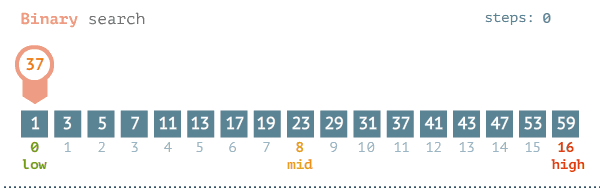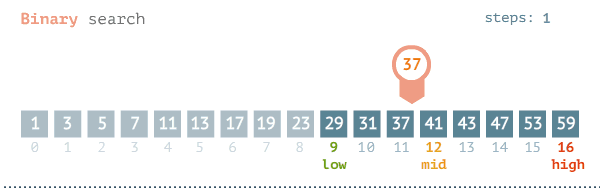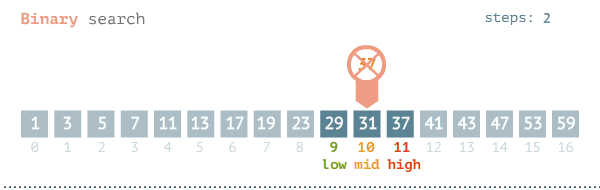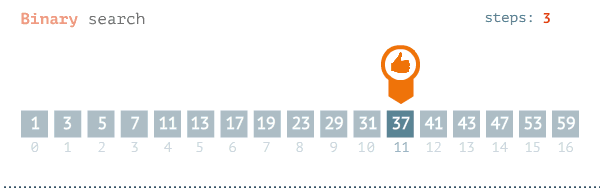
Binary search en yaygın kullanılan ve en hızlı arama algoritmalarından birisidir. O(logN) etkili olmasının nedenlerinden bir ise veri setinin büyüklüğü iki katına çıkarıldığında, işlem sayısı 1 artar.

Aşağıdaki görsellerde Binary search için en kötü ve en iyi senaryolar gösterilmiştir.

Binary Search için Büyük-O karmaşıklığı O(logN)’dır. Burada ufak bir hatırlatma yapayım O(logN) = O(log₂(N))’dir. yani 10 tabanında N logartiması değildir.

Javascript kodu şu şekildedir:



function binarySearch(dizi, arananDeger) {
  let baslangicIndex = 0;
  let bitisIndex = dizi.length - 1;
  let ortaIndex = Math.floor((baslangicIndex + bitisIndex) / 2);
  let tekrarSayisi=0;
  
  while (dizi[ortaIndex] !== arananDeger && baslangicIndex < bitisIndex) {
    if (arananDeger < dizi[ortaIndex]) {
      bitisIndex = ortaIndex - 1
    } else {
      baslangicIndex = ortaIndex + 1
    }
   ortaIndex = Math.floor((baslangicIndex + bitisIndex) / 2);
    tekrarSayisi ++;
  };
  console.log(`tekrar sayısı: ${ tekrarSayisi }`);
  
  return dizi[ortaIndex] === arananDeger ? ortaIndex : false;
};

console.log(binarySearch([1,22,44,66,77,78,79,80,84,90,96,99] , 90));

function binarySearch(dizi, arananDeger) {

let baslangicIndex = 0;

let bitisIndex = dizi.length - 1;

let ortaIndex = Math.floor((baslangicIndex + bitisIndex) / 2);

let tekrarSayisi=0;

while (dizi[ortaIndex] !== arananDeger && baslangicIndex < bitisIndex) {

if (arananDeger < dizi[ortaIndex]) {

bitisIndex = ortaIndex - 1

} else {

baslangicIndex = ortaIndex + 1

}

ortaIndex = Math.floor((baslangicIndex + bitisIndex) / 2);

tekrarSayisi ++;

};

console.log(`tekrar sayısı: ${ tekrarSayisi }`);

return dizi[ortaIndex] === arananDeger ? ortaIndex : false;

};

console.log(binarySearch([1,22,44,66,77,78,79,80,84,90,96,99] , 90));

binarySearch fonksiyonda 2–4 satır arasında bizin başlangıç index, bitiş index, ve dizinin orta elemanın index’i bulunuyor. 5. satırda tekrar sayısını ekrana yazdırmak için gerekli olan değişken tanımlanıyor(Bu tanımla isteğe bağlı. sadece tekrar sayısını göstermek istedim). 7 satırdaki while döngüsü aranan değer bulunana kadar tekrar edilecek şekilde ayarlanıyor(Aranan değer ile işlem yapılan index’e ait değer eşit değilse ve baslangıç index’i bitiş index’inden küçük kaldığı süre devam edilecek şeklinde ayarlanıyor). 8 ile 12. satırda orta index’in sol tarafında mı, sağ tarafında mı ona karar veriliyor. 13. satırda ortaIndex değeri yeni duruma göre yenileniyor. İstenilen durum sağlanana kadar döngü tekrar ediyor. 18. satırda aranılan değerin dizinin kaçıncı index’inde bulunduğu bilgisi dönülüyor.

O(logN)Karmaşıklığın grafiksel gösterimi şu şekildedir.

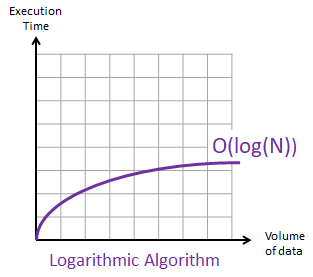
O(NlogN)

Bu karmaşıklığı anlatacak en iyi örnek, veri setinin sıralanması da kullanılan algoritmalarından biri olan Quicksort algoritmasıdır. Çalışma şekli şu şekildedir.

Sıralanacak bir sayı dizisini daha küçük iki parçaya ayırıp oluşan bu küçük parçaların kendi içinde sıralanması mantığıyla çalışır. Algoritma şu şekilde çalışır. Dizinin içinden bir eleman(genelde dizinin ilk elemanı yada son elemanı seçilir) eksen(pivot) olarak alır. Eksenden küçük olan sayılar eksenin önüne, büyük olan sayılar eksenin sonuna eklenir. Seçilen eksenin önündeki ve sonundaki sayılar yine aynı mantıkla küçük döngüler yapılarak sıralanır.

Aşağıda bu algoritmanın çalışma mantığı bulunmaktadır.

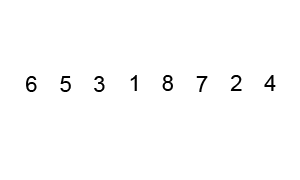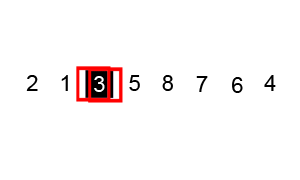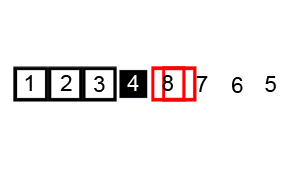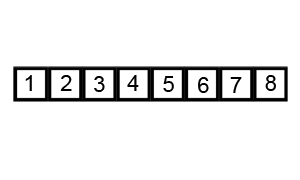
O(NlogN)Karmaşıklığın grafiksel gösterimi şu şekildedir.



 function quicksort(dizi) {
  if (dizi.length <= 1)
    return dizi;
  let eksen = dizi[0], sol = [], sag = [];
  for (let i = 1; i < dizi.length; i++) 
    dizi[i] < eksen ? sol.push(dizi[i]) : sag.push(dizi[i]);
  return quicksort(sol).concat(eksen, quicksort(sag));
};

console.log([1,4,8,5,0,3,65,78,89,23,56,54]);

function quicksort(dizi) {

if (dizi.length <= 1)

return dizi;

let eksen = dizi[0], sol = [], sag = [];

for (let i = 1; i < dizi.length; i++)

dizi[i] < eksen ? sol.push(dizi[i]) : sag.push(dizi[i]);

return quicksort(sol).concat(eksen, quicksort(sag));

};

console.log([1,4,8,5,0,3,65,78,89,23,56,54]);

Yukarıdaki örnekte 4. satırda eksen değeri ve bu eksenin sağında ve solunda tutulacak sayılar için iki dizi tanımlanıyor. 5. satırda dizinin boyu kadar döngü yapılıyor(Bu N karmaşıklığı). 6. satırda dizin i. elemanın eksenden büyük küçük olma durumuna göre ilgili diziye aktarıyor(Log(N)). 7. satırda öz-yineleme işlemi sol ve sağ diziler için ayrı ayrı yapılıyor karmaşıklığı. Sonuç olarak bu işlemin Big-O karmaşıklığı O(NlogN)’dır

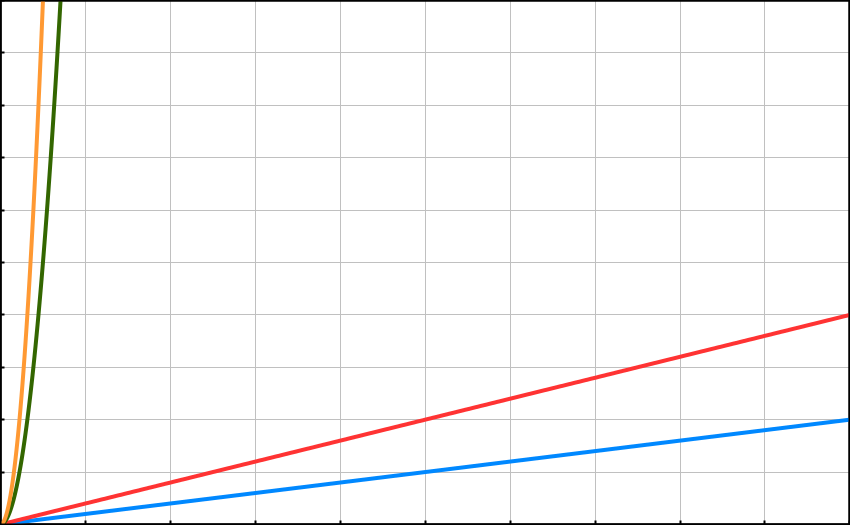
O(N) ve O(logN) Karmaşıklık Karşılaştırması

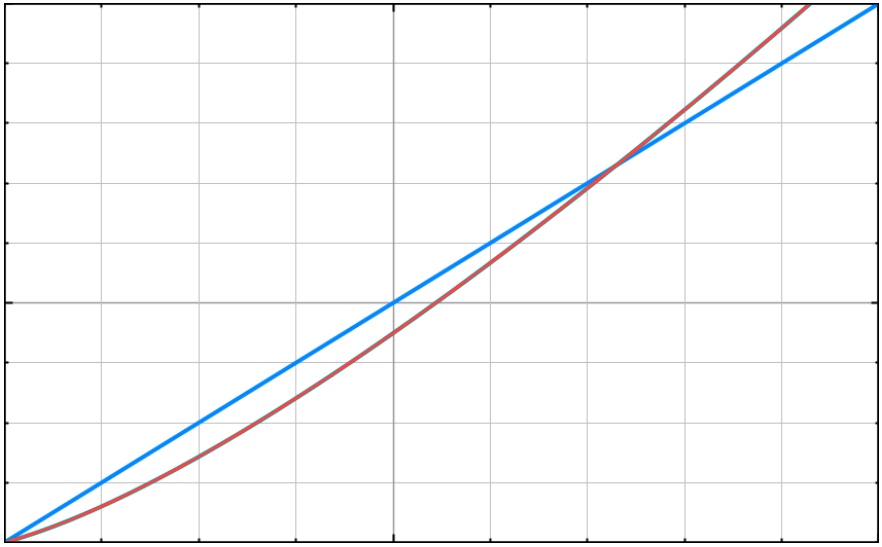
Hangi Algoritma daha iyi karşılaştırmasını yapıp ve geriye kalan son karmaşıklıktan bahsedip makaleyi bitireceğim. O(logN) karmaşıklığında veri setini 2 katına çıkarttığımızda işlem sayısı bir artmaktadır. ama O(N) karmaşıklığında işlem sayısı’da iki katına çıkar. Aşağıdaki grafikte bu durum daha net bir şekilde görülmektedir

Aşağıdaki görselde O(N) ve O(logN)(Bubble sort) karşılaştırılmaktadır. Average, Worst ve Best Case durumları görülmektedir

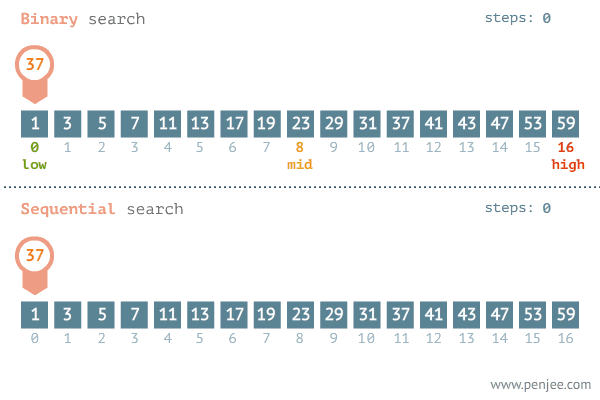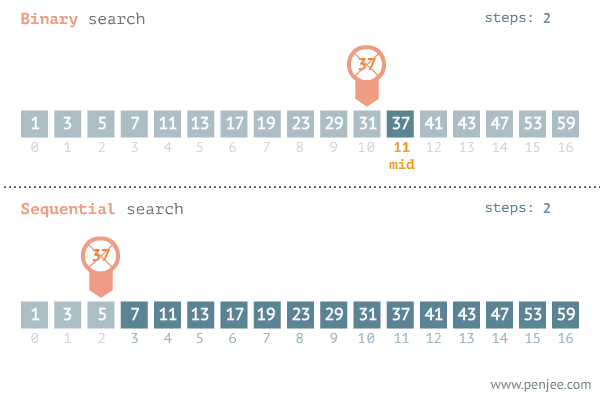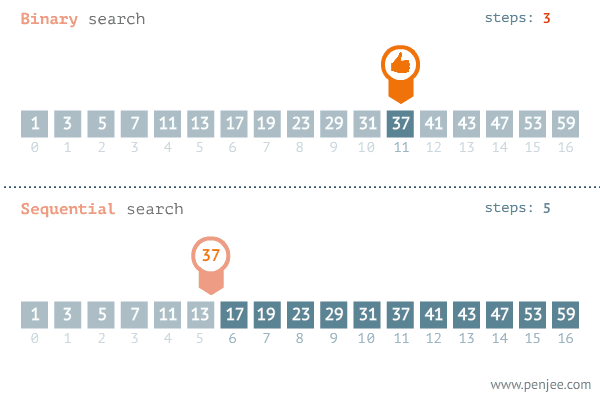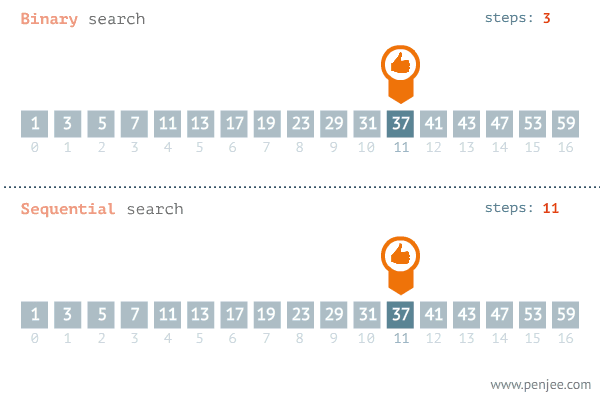
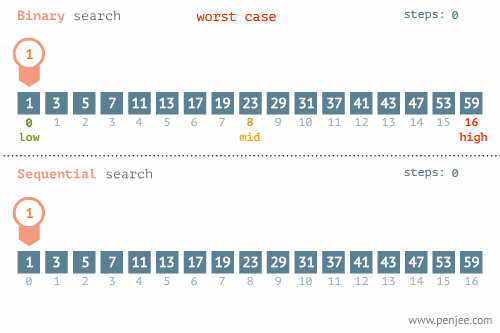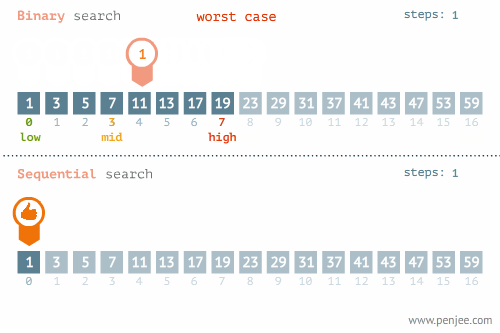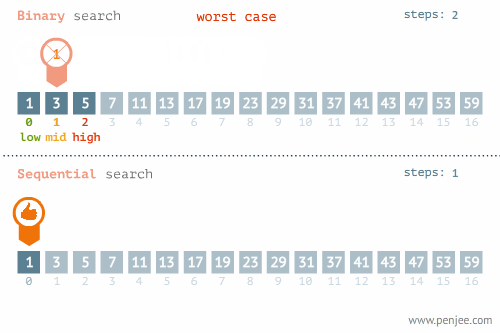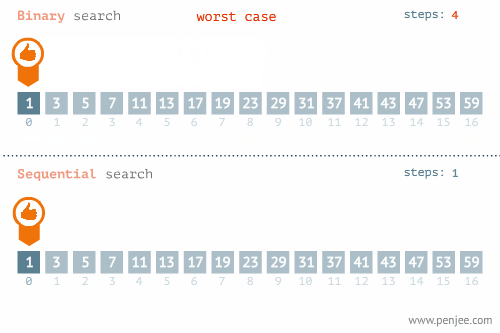
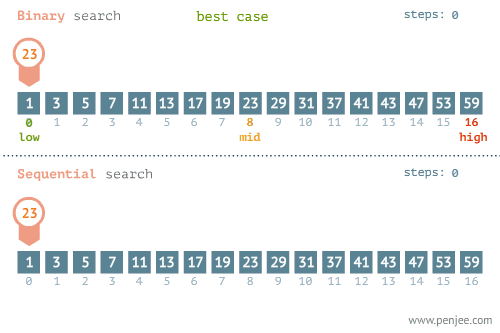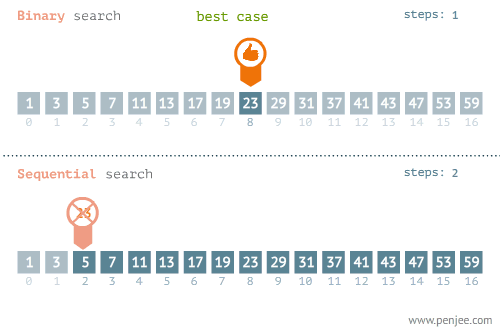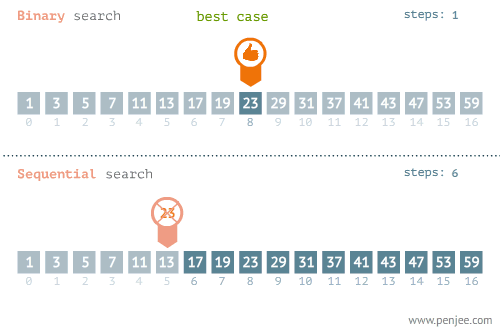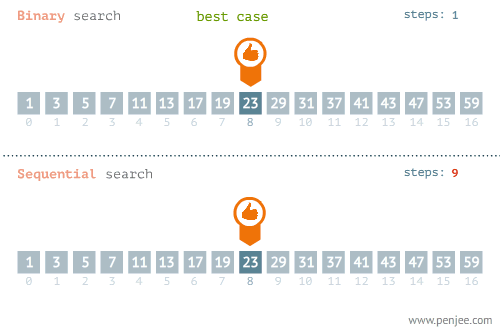
Yukarıdaki görsele baktığımızda best-case dışındaki diğer senaryolarda kazanan O(logN)’dır.

O(c^N): Exponential(Üstel) Karmaşıklığı

Girdi sayısı arttıkça işlem sayısı çok hızlı bir şekilde artan karmaşıklıktır. En tercih edilmeyen algoritmalardan birisidir.Bu karmaşıklığın en bilinen algoritması Gezgin Satıcı Problemi(Travel Salesman Problem). Üstel artışın ciddiyetini en güzel anlatan hikayelerden biri olan Hesap Bilmeyen Kral’ı okumanızı tavsiye ederim

Aşağıdaki örnekte konunun daha iyi anlaşılması için Fibonacci için javascript algoritması gösterilmiştir. Döngü yapmak yerine öz yineleme işlemi yapılıyor. Fibonacci için daha iyi algoritmalar mevcut ama üstel karmaşıklık için aşağıdaki kodu paylaşıyorum.



function fibonacci(sayi) {
  if (sayi <= 1) return sayi;
  return fibonacci(sayi - 2) + fibonacci(sayi - 1);
};
console.log(fibonacci(10)); // parametre değerini 100 yapınca olaylar çıkıyor :)

function fibonacci(sayi) {

if (sayi <= 1) return sayi;

return fibonacci(sayi - 2) + fibonacci(sayi - 1);

};

console.log(fibonacci(10)); // parametre değerini 100 yapınca olaylar çıkıyor :)

Yukarıdaki örnekte girdi olarak verilen sayı kadar öz-yineleme işlemi (5.satır) iki kere yapılıyor. 7. satırda 10 olarak verilen parametre 1 sayısına ulaşılana kadar öz yineleme işlemi yapılıyor.

Makaleyi bitirmeden önce son bir konudan bahsetmek istiyorum(Bitmeyen makale oldu ama önemli olduğunu düşünüyorum).

Büyük-O notasyonunda öz ardı edilen durumlar:

İşlem sayısı 3*n³ +2*n²+1 şeklinde bir algoritmanın Büyük-O karmaşıklığı O(N³)’dır. Peki neden sabit değeri(1) göz ardı edildi? Neden sadece en büyük üsse ifade(3*n³) alındı? en büyük üsse sahi olan idenin önünde çarpan(3) göz ardı edildi?

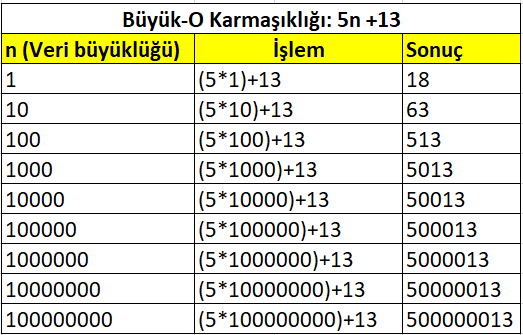
Yukarıdaki tablodan da görüldüğü bir veri setinin büyüklüğü arttıkça sabit değerin işlem sonucuna etkisi azalmaktadır. İfadenin sade olması için sabit değerler Büyük-O karmaşıklığında göz ardı edilir.

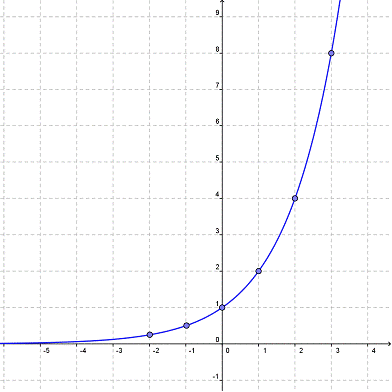
Benzer şekilde girdi sayısı arttıkça çarpan değerlerde göz ardı edilebilir. Aşağıdaki grafikte bu durum açıkça görülebilir.

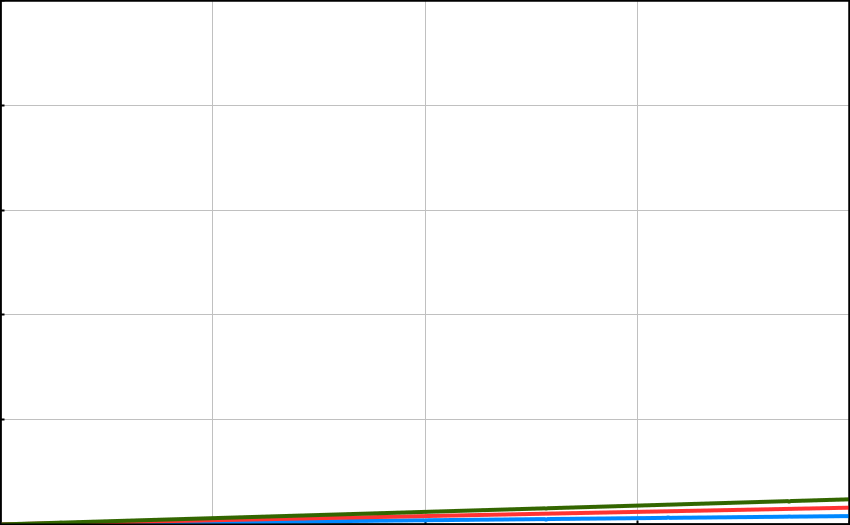
Küçük ölçekli veri setinde bu çarpan değerler önemlidir. Büyük-O gösterimi büyük ölçekli girdilerle ilgilendiği için çarpan değerler gösterimde kullanılmayabilir.

Son olarak en büyük üsse sahip ifadenin dışındaki diğer üslü ifadelerin neden göz ardı edildiğini gösterilen grafiğe bakalım

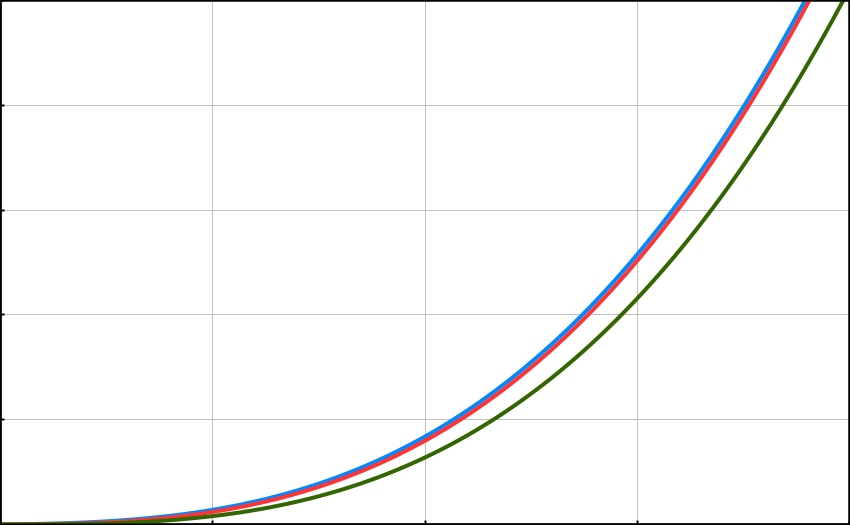
Kapanış

Uygulama neden yavaş? sorunusun cevaplarından birisini bu yazımda vermeye çalıştım. Bu yazı ile Veri yapıları ve Algoritmalar yazı serisine de giriş yapmış bulunuyorum. Yanlış ve anlaşılmayan olan durumları iletirseniz düzeltirim. Okuduğunuz için teşekkür ederim. Devam yazılarında görüşürüz.

Kaynaklar: