Lojistik Regresyon Neden Lineerdir?

By Şefik İlkin Serengil Last updated Ağu 18, 2021

Lojistik regresyon için genel yapılan bir yanlış algoritmayı non-lineer bir makine öğrenmesi algoritması olarak tanımlamaktır. Bu yazımızda bu yanlış anlaşılmanın nedenlerini açıklayacak, bir örnek üzerinde neden lineer olduğunu göstereceğiz. Son olarak da lineerliğinin dayandığı temel sebebi tartışacağız.

Sigmoid Fonksiyonu

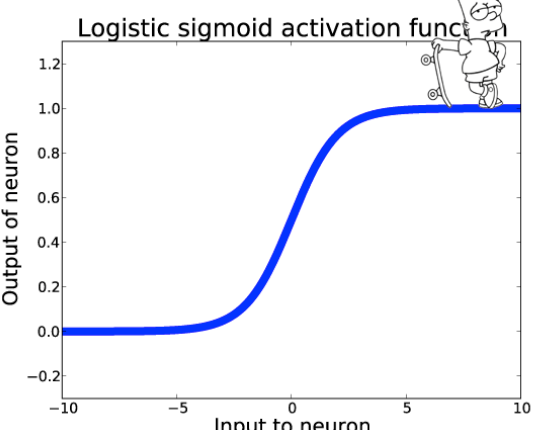
Bu yanlış anlaşılmanın temel nedeni algoritmanın kullandığı baz fonksiyon olan sigmoid fonksiyonun şeklidir. S şeklinde bir grafiğe sahip olan bu fonksiyon sizi algoritmanın non-lineer olduğuna dair bir yanlış yönlendirmede bulunabilir.

Sigmoid fonksiyonunun temel görevi sürekli aralıktaki girdileri [0, 1] arasında olasılık değerlerine dönüştürmektir. Formüldeki z ifadesi lineer regresyondan gelmektedir. Burada da yalnız başına sigmoid fonksiyonu algoritmayı non-lineer yapmaya yetmemektedir.

XOR Lojik Kapısı

İlerleyen bölümde neden algoritmanın non-lineer olduğunu tartışacağız ancak öncesinde kolay anlaşılması adına bir örnek üzerinde bunu inceleyelim. Bir algoritmanın lineer ya da non-lineer olduğunu anlamanın en kolay yolu onu bir non-lineer veri seti üzerinde test etmektir.

Burada xor lojik kapısı en basit non-lineer veri seti olma özelliğini taşımaktadır. Rastgele sınıflandırıcılar ve lineer yöntemler bu veri seti üzerinde %50 dolaylarında başarım elde ederken non-lineer yöntemler %100 başarı elde edebilmesi beklenmektedir.

Aşağıdaki python kod bloğu ile rastgele x-y değerlerinden oluşan bir xor veri seti elde edeceğiz.



import random
import pandas as pd

x_values = []; y_values = []; targets = []

for i in range(0, 4):
    if i == 0:
        sign_x = 1; sign_y = 1; target = 1
    elif i == 1:
        sign_x = -1; sign_y = 1; target = 0
    elif i == 2:
        sign_x = -1; sign_y = -1; target = 1
    elif i == 3:
        sign_x = 1; sign_y = -1; target = 0

    for j in range(0, 100):
        value_x = (5 + random.randint(0, 100)) * sign_x
        value_y = (5 + random.randint(0, 100)) * sign_y

        x_values.append(value_x)
        y_values.append(value_y)
        targets.append(target)

df = pd.DataFrame(x_values, columns = ["x"])
df["y"] = y_values
df["Decision"] = targets

import random

import pandas as pd

x_values = []; y_values = []; targets = []

for i in range(0, 4):

if i == 0:

sign_x = 1; sign_y = 1; target = 1

elif i == 1:

sign_x = -1; sign_y = 1; target = 0

elif i == 2:

sign_x = -1; sign_y = -1; target = 1

elif i == 3:

sign_x = 1; sign_y = -1; target = 0

for j in range(0, 100):

value_x = (5 + random.randint(0, 100)) * sign_x

value_y = (5 + random.randint(0, 100)) * sign_y

x_values.append(value_x)

y_values.append(value_y)

targets.append(target)

df = pd.DataFrame(x_values, columns = ["x"])

df["y"] = y_values

df["Decision"] = targets

Veriyi görselleştirirsek veri setinin içeriği daha kolay anlaşılacaktır.



for i in df['Decision'].unique():
    sub_df = df[df['Decision'] == i]
    if i == 1:
        color = 'blue'
    else:
        color = 'orange'
    plt.scatter(sub_df['x'], sub_df['y'], c = color)

for i in df['Decision'].unique():

sub_df = df[df['Decision'] == i]

if i == 1:

color = 'blue'

else:

color = 'orange'

plt.scatter(sub_df['x'], sub_df['y'], c = color)

Mavi noktalar doğru çıktıları temsil ederken turuncu noktalar ise yanlış çıktıları ifade etmektedir.

Lineer yöntemler veri setlerini doğrular ile ayırmayı denerken non-lineer yöntemler karar ağaçlarında olduğu gibi çok sayıda doğru veya nöral ağlarda olduğu gibi eğrilerle bunu yapmayı denemektedir. Görüldüğü üzere bu doğrusal olarak ayrılamayan bir problemdir. Bundandır ki non-lineer yöntemler bu basit problemi çözebilirken lineer yöntemler başaramamaktadır.

Lojistik Regresyon Modeli

Bu veri seti için bir lojistik regresyon modeli kuracağız. Noktalara ait x-y değerleri özniteliklerimiz olurken mavi ya da turuncu renklerle ifade edilen doğru / yanlış kararları da hedef değerlerimiz olacak.



from sklearn.linear_model import LogisticRegression
logres = LogisticRegression()
model = logres.fit(df[['x', 'y']].values, df['Decision'].values)

from sklearn.linear_model import LogisticRegression

logres = LogisticRegression()

model = logres.fit(df[['x', 'y']].values, df['Decision'].values)

Gördüğünüz gibi lojistik regreson, scikit-learn kütüphanesinin lineer model modülü altından yükleniyor. Algoritmanın lineer olduğu ile ilgili ilk ipucumuza sahibiz.

Model kurulduktan sonra eğitim setimiz üzerinde başarısını değerlendireceğiz. Lineer olduğuna inandığımız için başarının %50 dolaylarında olmasını bekliyoruz.



print("Skor: ",model.score(df[['x', 'y']].values, df['Decision'].values))

print("Skor: ",model.score(df[['x', 'y']].values, df['Decision'].values))

Skor fonksiyonu gerçekten de %50 başarı değerini döndürdü!

Skor: 50%

Peki Neden Lineer?

Lojistik regresyonun rastgele sınıflandırıcılar ile aynı başarıya sahip olduğunu bu basit xor lojik kapısı örneğinde göstermiş olduk. Bu algoritmanın lineer olduğunu gösteriyor peki ama neden?

Lojistik regresyon denklemini hatırlayalım.

y = 1 / (1 + e^(-z)) ve z = w0 + w1x1 + w2x2 + … + wnxn

Sonuç w katsayıları ve x girdilerinin çarpımının toplamına dayanmaktadır. Buradaki anahtar kelimeye odaklanalım: “toplam”. Sonucu kaysayıların çarpımı ya da bölümü olarak ifade edemiyoruz. Diğer bir deyişle denklem x1w1 * x2w2 şeklinde çarpımla ya da x1w1 / x2w2 şekinde bölümle ifade edilebilse, non-lineer bir algoritma olacaktı. İşte bu lojistik regresyonun lineer olmasının nedenidir.

İç içe yapılar ve gizli katmanlar, nöral ağları non-lineer yapmaktadır. Bununla birlikte karar ağaçları non-lineer yöntemler değillerdir ama uyguladığı parça parça lineer yaklaşım onu non-lineer veri setleri ile başa çıkmasını sağlamaktadır.

Bu yazı Why Logistic Regression is Linear yazısından Türkçe’ye çevrilmiştir.

lojistik sigmoid