En Kısa Yol Problemi ve Dijkstra Algoritması
En kısa yol problemleri, VLSI tasarımlarından örneklerde yer aldığı gibi proje değerlendirme çalışmalarında da kendisine yer verilen bir problem türüdür. Örnek verilecek olursa bir nakliye firmasının en az maliyetli taşıma ağını yapmasına yardımcı olur ya da bir şehir veya ülkenin su, doğalgaz vb ihtiyaçlarının, ihtiyaç sahiplerine en az maliyetle ulaşmasında büyük rol oynar. Bilgisayar üzerinde yer alabileceği alanlardan bir kaçı da internet ağ trafiği protokolü yönlendirme ve oyun programlamaladır.
Problemi çözmek üzere tarihte ortaya çeşitli algoritmalar atılmıştır. Bunlardan en verimsizi kaba kuvvet algoritması olarak adlandırılan, bütün yolların hesabı yapıldıktan sonra en kısa yolun belirlenebildiği bir algoritmadır. Bu yöntem az adette düğüme sahip problemlerin çözümünde işlem görebilmiş olsa bile düğüm sayısı arttıkça da bir o kadar verimsiz bir yapıya bürünür. En kısa yol problemleri üzerine geliştirilmiş ve benim de bu yazımda anlatacağım diğer algoritma ise Dijkstra algoritmasıdır. Dijkstra algoritması adını Hollandalı matematikçi ve bilgisayar uzmanı Edsger Dijktra’dan almıştır. Dijkstra ayrıca for, while gibi döngülerin ortaya çıkarılmasında pay sahibidir.
Algoritmanın İşleyişi
Dijkstra algoritması prensibi gereği kaynak noktasına ihtiyaç duyar ve etiketleme yöntemi ile çalışır. İki çeşit etiketleme mevcuttur bunlardan biri geçici diğeri ise kalıcı etiketlemedir. Geçici etiketleme yaparken iki düğüm arası mesafe hesaplanır ve yazılır. Sonraki süreçte yapılan hesaplamalarda daha kısa bir yola rastlanmaz ise geçici etiket, kalıcı etiket olarak adlandırılmaya başlar. Şayet başka bir erişimde olan yol daha kısa mesafeye sahipse yeni yol kalıcı etiket olmaya başlar. Etiketleme aşamasını öncelikle kısa bir örnek üzerinde değerlendirelim.
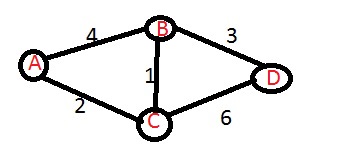
Şekildeki gibi basit bir 4 düğümlü grafımız olduğunu farz edelim. Adım adım çözüm yapalım ve çözüm için kaynağımız A düğümü olsun.
- A noktasından B ye geçerken geçici etiket olarak 4 elde edilir. (A->B),( ∞, 4)
Tanımlamada 4 geçici etiketi, ∞ ise kalıcı etiketi temsil eder.
A noktasından C ye geçerken geçici etiket olarak 2 elde edilir. (A->C), (∞ , 2)
Şimdiki adım ise geçici ve kalıcı etiketler arasındaki ilişkiyi belirleyecek adımdır ki önemli bir adım olduğunu söyleyebilirim. Kalıcı etiket ve geçici etiket matematiksel olarak kıyaslanır;
Koşul 1) Eğer kalıcı etiket geçici etiketten küçük ise kalıcı etiket aynen kalır.
Koşul 2) Eğer geçici etiket kalıcı etiketten küçük ise geçici etiket kalıcı etiket olarak ayarlanır.
Mevcut durumda etiketler (A->B),(4, ∞) ve (A->C),(2, ∞) olarak ayarlanacaktır.
Sıradaki işlemde gelinen düğümler için 1. İşlem yinelemeli olarak gerçekleştirilecektir.
Bu grafta önem teşkil eden nokta olan (A->B) yolu için bir hesap daha ilerletelim ve C noktasının komşusu olan B noktasına ulaşımını ele alarak yorum yapalım.
(C->B) yolunun uzaklığı 1 yani etiketleme işlemi bu aşamada (C->B), (∞ ,1) olacaktır.
(A->B) etiketlemesi tekrar ele alınmak durumundadır çünkü A düğümünden yola çıkılıp B noktasına varılan bir başka yol elde ettik bu yol da A->C->B yoludur. İlk işlemde elde edilen etiketleme (A->B),(4, ∞ ) şeklindeydi. Sırada elde edilen “aktarmalı” yol için hesap yapacak olursam (A->C),(2, ∞ ) + (C->B),(1, ∞ ) yani 2+1 işlemi sonucunda yeni A->B etiketlemesi (A->B),(4,3) olacak şekilde düzenlendi. Bu durumda geçici etiket, kalıcı etiketten daha küçük bir değere sahip olduğu için A->B arası en kısa mesafe 3 olarak değiştirildi ve (A->B),(3, ∞ ) son etiketlemesi elde edildi.
Yinemeli işlemler sonunda A kaynak noktasından diğer noktalara en kısa nasıl ulaşabilirim sorusuna yanıt bulmuş olacaksınız. Bu kısa örnek için son olarak cevapları yazacağım eğer ki kendi çözümlerinizde bir farklılık olursa ve eminseniz yorum olarak söyleyebilirsiniz incelenip düzeltilecektir.
(A,B)->3, (A,C)->2, (A,D)->6
Dijkstra Algoritması Örnek
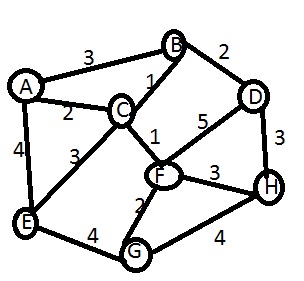
Şekilde verilen kısmen biraz daha karışık graf üzerinde A noktasını başlangıç noktası (kaynak) kabul ederek diğer noktalara en kısa ulaşım yollarını inceleyelim.
A->B=3, A->C=2, A->E=4
A noktasının bütün komşuları üzerinde incelemeyi gerçekleştirdik. Şimdi sırayla A noktasının komşularının komşuları ile olan uzaklıklarını inceleyelim.
E noktası için inceleme
E->G=4, E->C=3
E->C yolu için A->C yolu incelemesi yapılmalıdır bu durumda A->C=(2,4+3) geçici ve kalıcı etiket ikilisi elde edilir. 2<7 olduğu için A->C yolu 2 olarak kalır.
C noktası için inceleme
C->E=3, C->F=1, C->B=1
A->C->E yolu 5 olduğu için A->E yolunda yine bir değişiklik yapmayacağız ve 4 olarak kalacak.
A->C->B yolu 3 ve A->B yolu da bu değere (3) eşit, yine herhangi bir değişiklikte bulunmamız gerekmiyor.
B noktası için inceleme
B->D=2, B->C=1
İncelendiği zaman yine herhangi bir değişiklik gerektiren durum olmadığı görülecektir.
Şimdi de ulaşım sağlamış olduğumuz G, F, D yolları ve komşuları arasında inceleme yapacağız.
F noktası için inceleme
F->G= 2, F->H =3, F->D=5
G noktasının ulaşım yollarını incelemeye alındığı zaman önceki incelemede A->E->G =8 olarak bir kalıcı etiket oluşturmuştuk, şimdi A->C->F->G =5 alternatif yolu geçici etiket olarak oluşacak bu durumda A->G,(8,5) etiketlemesi üzerinden yapılacak işlemde 8>5 olduğu için kalıcı etiketimiz 5 değerine değiştirilecek.
Sonuç itibariyle A noktasının diğer noktalara en kısa ulaşım yolları aşağıdaki gibi olacaktır.
A->G=5
A->H=A->C->F->H=6
A->D=5
A->F=3
A->E=4
A->C=2
A->B=3
Kendi inceleme ve çözümünüzden sonra sonuçlarda bir farklılık elde ederseniz yorum olarak belirtebilirsiniz ve alıştırma yapmak için kendi yarattığınız graflar üzerinde incelemede bulunmanız yararınıza olacaktır.

