Graf Teorisi ve Königsberg’in Yedi Köprüsü Problemi
Graf teorisi bilgisayar ile yapılan modellemelerin çoğunda önemli bir yer tutmaktadır. Genelde graflar üzerine kurulmuş ve graf teorisi ile çözümlenen problemler karmaşık yapıya sahip olduklarından graf teorisi bilgisayar programcılığının en önemli alanları arasında yer alır. Genel anlamda kullanım amaçlarından en önemlisi iki nokta arasında bulunan güzergah veya somut bir bağlantı bulunmak istenmesidir. Graf teorisinin başlıca uygulandığı alanlar olan bilgisayar bilimleri (veri yapıları, görüntü işleme, yapay zeka, ağlar), biyoloji, fizik, tarih, matematik, dilbilgisi, iletişim teknolojileri, bilişim sistemleri vb alanlar bir önceki cümlede verilen tanımla ilgili problemleri fazlasıyla içinde barındıran alanlardır.
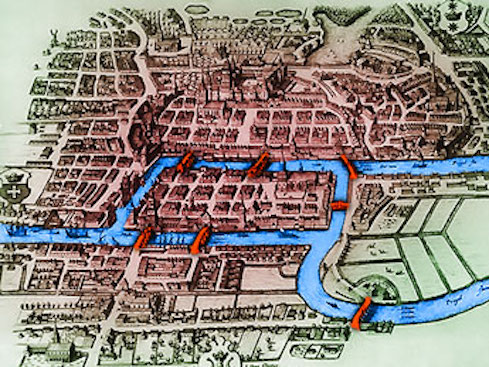
Graf teorisinin ortaya çıkışı veya temellendirildiği olay için genel görüş 1736 yılında Euler tarafından çözüme kavuşturulmuş daha doğrusu yanlışlığı doğrulanmış olan Königsberg Köprüsü problemidir. Bu problem Prusya’da yaşayan meraklı halk tarafından ortaya çıkmıştır. Königsberg şehrinde yaşayan halkın dikkatini çeken Pregel ırmağı ve ırmağın meydana getirdiği bir ada ve bir yarımadayı birbirine bağlayan 7 adet köprü olmuştur.
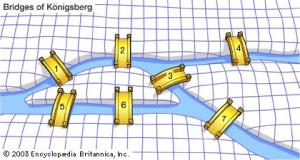
Problemi detaylandıracak olursak, kent halkı yukarıdaki fotoğrafta gördüğünüz şehri her köprüden bir ve sadece bir kez geçerek bütün şehri dolaşabilir miyiz sorusu üzerinden kendilerine hem bir uğraş hem de bir oyun geliştirdiler. Yıllarca süren uğraşlar sonunda kimse olumlu bir sonuç elde edemedi. Sonraki süreçte bu kent ve halkın ortaya attığı teori Euler’in dikkatini çekti ve Euler kent içinde köprü köprü gezmek yerine kalem ve kağıt üzerinde bu problemi ele aldı. Euler tabi ki kağıt üzerine fotoğraftaki gibi bir şekil yerine altta vermiş olduğum belki de ilk graf denilebilecek şekli çizdi.
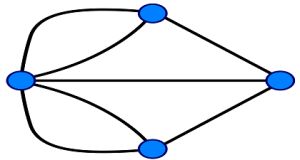
Bu şekil üzerinden çalışmalarını yapan Euler bir süre sonra bu teorinin mümkün olmayacağına ikna oldu ve hangi durumlar olsaydı mümkün olurdu üzerinde çalışmalar yaparak problemin çözümünü dönemin ünlü matematik ve bilim dergilerinde yayımlattı.
En basit anlamda ifade ile Euler’in çözümü köşelerin dereceleri üzerinde temellendi. Başlangıç köşesi eğer son nokta olma şartı altında değilse (çıkış),(çıkış,dönüş,çıkış),(çıkış, dönüş, çıkış, dönüş, çıkış),.. şeklinde tek sayıda derece sahip olması gerekiyordu ve aynı zamanda son nokta da başlangıç noktasının ikizi gibi davranmalı ve tek dereceli olmalıydı. Orta köşeler ise çift dereceli olmalıydı ki çıkış ve dönüş yolları eşit miktarda olabilsin. Sonuç olarak sahip olduğumuz grafta 2 adet tek sayı dereceli köşe ve diğer köşeler de çift sayı dereceli ise bütün köşeler köprülerin her birinden bir ve sadece bir kez geçilme koşulu altında gerçeklenebilir.
Eğer problem bizden başlangıç noktasını aynı zamanda bitiş noktası olarak ta isterse önceki problemde elde edilen başlangıç ve bitiş noktaları arasında bir yol daha çizmek olacak. Bu durumda grafın sahip olduğu bütün köşeler çift dereceli olacak.
Graflarla ilgili güzel bir problemin çözümünün ardından kısaca graf teorisinin gelişiminde söz sahibi bilim adamlarına değinecek olursam;
1) 1736-Leonard Euler
“Königsberg’in yedi köprüsü” makalesini yayımlayarak graf teorisinin başlangıcını oluşturup topoloji-graf ilişkisini ortaya çıkardı.
2)1822-James Joseph Slyvester
İlk kez “graf” sözcüğüne yer veren isim.
3)1845-Gustav Kirchhoff
Fizik ve elektrik alanında da grafların yeri olduğunu gösteren Kirchhoff elektrik devrelerinde akım ve gerilim hesabı üzerine oluşturduğu meşhur kuramları yayımladı.
4)1852-Francis Guthrie
4 renk problemini ortaya attı.
5)1927-Pontryagin 1930-Kazimierz Kuratowski
VLSI teknolojisi teknolojilerinin önemli yardımcısı olan düzlemsel grafların özellikleri keşfedildi.
6)1936-Denes König
Graf teorisini konu alan ilk kitap yayımlandı.
7)1976-Kenneth Appel, Wolfgang Haken
Uzun süreli bilgisayar ortamında süren hesaplamalar sonunda harita renklendirmesinde 4 rengin gerekli ve yeterli olduğunu kanıtladılar.