RSA’nın Hegemonyasını Yıkmak: GPG’nin Yeni Varsayılanlarında Eliptik Eğri Kriptografisi

Kriptografi dünyasında, çok az algoritma RSA kadar baskınlık ve güven kazanmıştır. Neredeyse 50 yıl boyunca RSA (Rivest-Shamir-Adleman), dijital imzalardan güvenli iletişimlere kadar her şeyi güçlendiren açık anahtarlı kriptografinin temel taşı olmuştur. Ancak dijital ortam geliştikçe ve hesaplama gücü arttıkça, RSA’nın bir zamanlar sarsılmaz olan konumu artık sorgulanmaktadır.

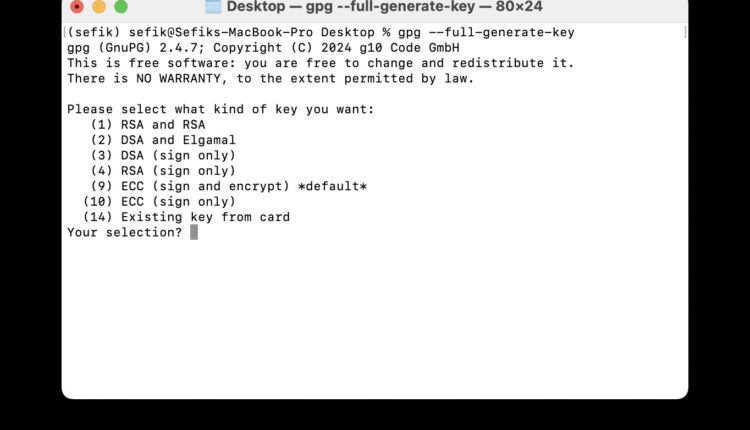
GPG’nin (GNU Privacy Guard) son sürümü, varsayılan olarak eliptik eğri tabanlı algoritmaları benimseyerek önemli bir değişikliğe gitmiştir—özellikle, şifreleme için ECDH (Eliptik Eğri Diffie-Hellman) ve imzalar için EdDSA (Edwards-eğrisi Dijital İmza Algoritması). Aslında, GPG sürüm 2.1’den beri eliptik eğri kriptografisini (ECC) desteklemekteydi, ancak 2.3 sürümüyle birlikte artık varsayılan olarak ECC anahtar çiftleri üretmeye başlamıştır. Bu değişiklik, RSA’nın hegemonyasının sonunu işaret etmektedir; çünkü eliptik eğri kriptografisi (ECC), çok daha yüksek verimlilikle aynı güvenlik seviyesini vaat etmektedir.

RSA’nın matematiksel sadeliği onu anlamayı kolaylaştırmış ve hem şifreleme hem de dijital imzalar için aynı algoritmanın kullanılabilmesi önemli avantajlar sağlamıştır. Ancak, gerçek dünya uygulamalarında RSA oldukça yüksek hesaplama maliyetine sahiptir. Öte yandan, insan açısından kavraması daha karmaşık olan ECC (Eliptik Eğri Kriptografisi), modern bilgisayarlarda çok daha verimli çalışır; daha küçük anahtar boyutları ve daha hızlı işlemler sunarken güvenlikten ödün vermez.

Bu blog yazısı, GPG’nin bu değişime yönelmesinin teknik nedenlerine derinlemesine bir bakış sunacak; ECC’nin nasıl çalıştığını, RSA’ya kıyasla sunduğu avantajları ve neden kriptografinin geleceği olduğunu inceleyecek

RSA’dan ECC’ye Geçiş

On yıllar boyunca RSA, dijital iletişimleri güvence altına almak ve imzaları doğrulamak için başvurulan algoritma olmuştur. Bu kadar yaygın benimsenmesinin nedenlerinden biri, altında yatan matematiğin sadeliğidir. RSA, güvenliğini büyük sayıların çarpanlarına ayrılmasının zorluğuna dayandırır—bu da yüksek seviyede anlaşılması nispeten kolay bir fikirdir. Ayrıca aynı algoritmayı hem dijital imza, hem anahtar değişimi hem de mesaj şifreleme için kullanabiliyorduk.

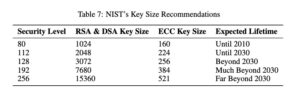
Ancak bu sadelik, bir bedelle gelir. RSA’nın güvenliği doğrudan anahtar boyutuna bağlıdır; anahtar ne kadar büyükse, algoritma o kadar güvenlidir. Fakat zamanla hesaplama gücü arttıkça, gereken anahtar boyutu da artmıştır. Örneğin, 256 bitlik bir ECC anahtarının sunduğu güvenlik seviyesine ulaşmak için, RSA anahtarının 3072 bit veya daha büyük olması gerekir ki bu da RSA’yı hesaplama açısından maliyetli ve daha yavaş hale getirir.

Bu hesaplama darboğazı, modern sistemler, mobil cihazlar ve IoT aygıtları daha verimli kriptografik çözümler talep ettikçe daha da belirgin hale gelmiştir. Ayrıca, RSA’nın imzalama ve şifreleme işlemleri daha fazla enerji tüketir, bu da batarya ile çalışan cihazlar için bir sorun oluşturur.

Şifreleme

ECDH aslında bir anahtar değişim algoritmasıdır, yani temel amacı iki taraf arasında güvenli bir şekilde paylaşılan bir sır oluşturmayı sağlamaktır. Her ne kadar ECDH, her iki tarafın (Alice ve Bob) hesaplama yapmasını gerektirse de, GPG bu süreci arka planda sorunsuz bir şekilde yönetir. Böylece, her iki taraf güvenli bir şekilde ortak bir sır oluşturabilir ve bu sırrı mesajları şifrelemek için kullanabilir; tüm bunlar eliptik eğri kriptografisinin (ECC) verimlilik ve güvenlik avantajlarıyla birlikte gerçekleşir.

Anahtar Oluşturma

ECDH (Eliptik Eğri Diffie-Hellman) anahtar değişim protokolünde, hem Alice hem de Bob, eliptik eğri matematiğine dayalı olarak kendi özel ve açık anahtarlarını oluştururlar.

Alice’in özel anahtarı: da – rastgele bir tamsayı
Bob’un özel anahtarı: db – rastgele bir tamsayı
G: Ortak eliptik eğri E üzerinde önceden tanımlanmış bir açık nokta

Eğri

GPG varsayılan olarak Edwards formuna ait bir eliptik eğri olan ed25519 eğrisini varsayılan olarak kullanmaktadır. Bu eğrinin denklemi şu şekildedir:

-x² + y² = 1 – (121665/121666) x²y² (mod 2²⁵⁵ – 19)

Eğrinin ismindeki 25519 eliptik eğrinin üzerinde tanımlı olduğu asal alandan gelmektedir (bknz mod).

Ed25519 eğrisinin önceden tanımlı baz noktası şu şekildedir:

GPG, Edwards eğrilerini kullanmak zorunlu değildir. Örneğin, GPG aynı zamanda eliptik eğrilerin Weierstrass formuyla tanımlanan NIST eğrilerini de destekler. Temelde, bir eliptik eğri E sadece matematiksel bir denklemdir.

Açık anahtarların hesaplanması

Alice ve Bob kendi gizli anahtarlarını kullanarak seçilen eliptik eğri üzerindeki karşılık gelen noktaları hesaplar. Bu noktalar kendilerinin açık anahtarları olacaktır.

• Alice’in açık anahtarı: Qa = da x G
• Bob’un açık anahtarı: Qb = db x G

Hesaplama Qa=da×G olduğunda, G’nin eliptik eğride herkesçe bilinen bir nokta olduğunu ve x ile y koordinatlarıyla temsil edildiğini unutmamak önemlidir. İlk bakışta bu, bir skaler ile bir noktanın basitçe çarpılması gibi görünebilir ve bu da kafa karıştırıcı olabilir.

Ancak, bu işlem aslında eliptik eğri üzerinde bir skaler çarpma işlemidir ve bu işlem, G noktasının kendisiyle defalarca eklenmesini içerir. da×G hesaplamak için eliptik eğrilerin toplama kuralını kullanırız. Bu kural, eğrideki iki noktanın nasıl birbirine eklenebileceğini ve yeni bir nokta üretebileceğini tanımlar. Bu ekleme işlemini tekrar ederek, G noktasını skaler da ile çarpmış oluruz.

Özetle, Qa yine eliptik eğride bir başka noktadır. Bu hesaplamanın nasıl yapıldığını merak ediyorsanız, aşağıdaki yazılara göz atabilirsiniz:

• Eliptik eğrilerin toplama kuralının matematiği: Weierstrass formu, Koblitz formu, Edwards formu, Twisted Edwards formu.
• Python LightECC kütüphanesi ile toplama ve çarpma operatörlerini kullanarak bu hesaplamayı basitçe yapabilirsiniz.
• Verilen eliptik eğri formu için toplama ve ikiyle çarpma formüllerine sahipseniz, verilen k ve G için da×G’yi kolayca çift ve ekle yöntemiyle hesaplayabilirsiniz.

Öte yandan, verilen Qa ve G çiftinden da’yı geri elde etmek zor bir problemdir. Dikkat edilmesi gereken bir diğer önemli nokta, Qa’nın Alice’in açık anahtarı ve G’nin önceden tanımlanmış herkes tarafından bilinen bir nokta olduğu, ancak da’nın Alice’in özel anahtarı olduğu ve bunun kamuya açıklanmadığıdır.

Alice

Diyelim ki Alice, Bob’a güvenli ve şifreli bir mesaj göndermek istiyor ve şifreleme için ECDH kullanıyor. Her ne kadar ECDH aslında bir anahtar değişim algoritması olsa da, bu algoritmadan türetilen paylaşılan gizli bilgi, şifreleme için kullanılır.

• Alice, göndereceği mesajı şifrelemek için rastgele bir AES anahtarı üretir (buna K diyelim).
• Alice, mesajı rastgele üretilen AES anahtarıyla şifreler (buna Cm diyelim).
• Alice, gizli anahtarı da’yı ve Bob’un açık anahtarı Qb kullanarak bir paylaşılan gizli anahtar hesaplar. Buna Sa diyelim. Hesaplaması şu şekilde olacak Sa=da×Qb.
• Sa, Bob tarafından da hesaplanabilecektir. Buna sonraki bölümde değineceğiz.
• Alice, rastgele üretilen AES anahtarı K’yı Sa’yı kullanarak şifreler (buna Ck diyelim). Şifrelenmiş AES anahtarı, şifreli mesaj ve Alice’in açık anahtarı Bob’a gönderilir.

Özetle, Alice Bob’a şu ikiliyi gönderir: (Cm,Ck,Qb)

Bob

• Bob, Alice’in şifreli mesajını (Cm), şifrelenmiş AES anahtarını (Ck) ve Alice’in açık anahtarını (Qa) aldığında, kendi gizli anahtarı db ve Alice’in açık anahtarı Qa’yı kullanarak kendi paylaşılan anahtarı Sb’yi hesaplar: Sb=db×Qa
• ECDH algoritmasının eliptik eğrilerin matematiksel özellikleri sayesinde Sa ve Sb eşit olur. Yani, Bob da Alice’in AES anahtarını şifrelemek için kullandığı aynı paylaşılan sırrı elde etmiş olur. Bob bu paylaşılan gizli anahtarı kullanarak şifrelenmiş AES anahtarını (Ck) çözer ve orijinal AES anahtarını (K) elde eder.
• Bob, artık elinde K olduğuna göre, Alice’in gönderdiği şifreli mesajı (Cm) bu anahtar ile çözüp orijinal mesaja ulaşabilir.

Yeni İmza Algoritmaları

ECDH’ye ek olarak, GPG’nin yaptığı bu değişiklik, eliptik eğri tabanlı imza algoritmalarını da beraberinde getiriyor: ECDSA (Eliptik Eğri Dijital İmza Algoritması) ve EdDSA (Edwards-eğrisi Dijital İmza Algoritması). Bu iki imza yöntemi de eliptik eğri kriptografisine dayanır ve RSA ile aynı güvenliği daha yüksek performansla sunar.

• ECDSA: ECDSA, Bitcoin ve TLS/SSL gibi sistemlerde dijital imzalar için yaygın olarak benimsenmiştir. Güçlü bir güvenlik sunsa da, yan kanal saldırılarına karşı hassasiyet gibi bazı performans sınırlamaları vardır.
• EdDSA: EdDSA, ECDSA’ya göre daha modern, daha güvenli ve daha verimli bir algoritmadır. Yan kanal saldırılarına karşı daha iyi dayanıklılık sağlar ve hem donanımda hem de yazılımda yüksek performans için tasarlanmıştır. GPG’nin EdDSA’yı varsayılan imza algoritmalarından biri olarak benimsemesi, sistemin güvenliğini ve performansını artırmaktadır.

Sonuç

GPG’nin varsayılan olarak ECDH ve EdDSA’ya geçme kararı, kriptografik uygulamalarda kritik bir evrimi temsil ediyor. Eliptik Eğri Kriptografisi’nin (ECC) benimsenmesiyle GPG yalnızca performansını artırmakla kalmadı, aynı zamanda daha yüksek güvenlik ve verimlilik sunan modern kriptografi standartlarıyla da uyum sağladı.

RSA onlarca yıl boyunca bize iyi hizmet etti ancak artan hesaplama gücü karşısında sahip olduğu sınırlamalar, geleceğin kriptografik sistemlerini güvence altına almak için daha az uygun hale getiriyor. ECC ve onun türevleri olan ECDH ve EdDSA’ya geçiş, GPG’nin dijital iletişim ve veri gizliliği alanında değişen ihtiyaçlara karşı güncel ve güvenli bir çözüm olarak kalmasını sağlıyor.

Daha bağlantılı bir dünyaya doğru ilerlerken, hız, verimlilik ve güvenliğin ön planda olduğu bu çağda, ECC tabanlı kriptografi; iletişimimizin gizli, güvenli ve etkili kalmasında öncü rol oynayacaktır.

Referans

S. I. Serengil, Breaking RSA’s Hegemony: Elliptic Curve Cryptography in GPG’s New Defaults, 2024 Aralık.