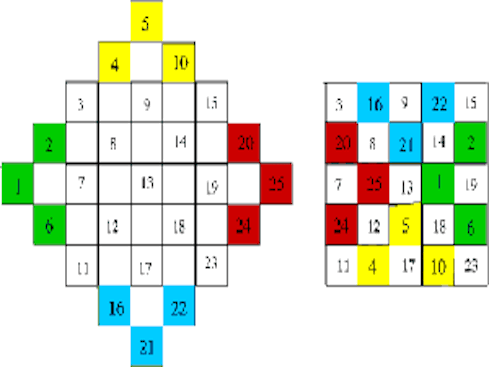
Sihirli Kareler ve 8 Vezir Problemi ile İlişkisi
Sihirli kareler, uzun yıllardır matematikçiler arasında gizemliliğini korumaya devam eder. Çin, Yunanistan, Hindistan, Mısır ve Roma gibi eski medeniyetlerin üzerinde uğraştığı ve bilgisayarın icadından sonra daha farklı problemlere cevap olmuşlardır. Satır, sütun ve köşegenlerinde yazılı olan sayıların toplamı birbirine ve bir sabite eşit olan karelerdir. Sabit sayıyı elde etmemizi sağlayan formül ise n:bir kenarın parça sayısı olmak üzere n*(n2+1)/2 şeklindedir.
Karelerin insan eliyle çizimi
1)Tek sayıda kenar parçası olan kareler(7*7 gibi)
Tek sayıda kenar parçasına sahip karelerin insan eliyle çizilmesinde bize baklava dilimi yardımcı olacak.
Öncelikle kenar sayısı adetinin karesi kadar kareden oluşan karemizi oluşturalım. 5*5 kareyi örnek olarak yapacağız.

Sonrasında karemizin ortada kalan elamanlarını içine alacak şekilde bir baklava çiziyoruz.
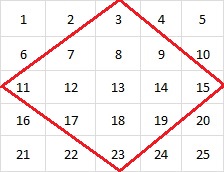
Bir ileri adımda çektiğimiz köşegenleri bütün kareler için uyguluyoruz.
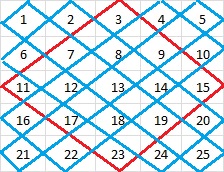
Sonrasında kırmızı köşegenler arasında kalan kareyi, sihirli karemizin iskeletini oluşturacak şekilde yazıyoruz.

Boşlukları Doldurma
Boşlukları doldurma aşamasında geometri, analitik veya fizik optik derslerinde görmüş olduğumuz yansıma özelliğini kullanıcaz ve arta kalan sayıları baklava içindeki boş kalan yansıma karelerine yerleştireceğiz. Burada kritik noktamız ise şu, yansıma işleminde birebir yansıma yapmayacağız sadece çizeceğimiz orta köşegenlerin diğer tarafına yazacağız.
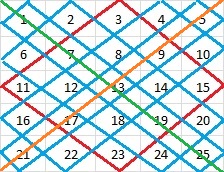
Orta köşegenleri şekildeki gibi yeşil ve turuncu renkler ile çizdik, şimdi sayıları yerleştirelim. 21 sayısı yeşil köşegenin altında olduğu için baklava diliminin yeşil köşegeni üzerinde kalan kareye yerleşecek. Bu şekilde yansıma işlemlerinin sonucunda elde edilecek en son sihirli karemiz aşağıdaki gibi olacaktır.
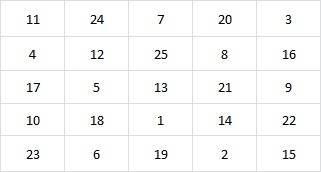
Unutmayalım bu yöntem, sihirli kare elde etme yöntemlerinden sadece bir tanesidir, ve en kolayıdır. Ve ayrıca bu sihirli kareyi kullanarak kare üzerinde satır ve sütun değişiklileri uygulayarak yeni sihirli kareler elde edebilirsiniz. Bu işlem için toplamları koruma şartı ise i. Satır ile (n+1-i). Satır ve arkasından da i. Sütun ile (n+1-i). Sütunun yer değiştirmesidir.
8 Vezir Problemi ve Sihirli Kareler ile İle İlişkisi
Problemin içeriği bir satranç tahtasına 8 adet vezir konulacak ve bu vezirler hiçbir şekilde oyun kurallarında geçerli olan vezir hareketleri ( düz ve çapraz) hareketler neticesinde birbirinin yoluna çıkmayacaktır. Çözümler sonucunda tahmin edildiği gibi bir satır ve bir sütunda sadece 1 vezir olması gerektiği görülmüştür. Bazı örnek 8 vezir çözümleri.

Şekillerden de görüleceği üzere vezirlerin yerleştirildiği karelerin sayısal toplamları 260 değerine eşit olmaktadır. 260 sayısı aynı zamanda 8*8lik bir sihirli karenin köşegen, satır ve sütunlarının alması gereken sabit değer olmaktadır.