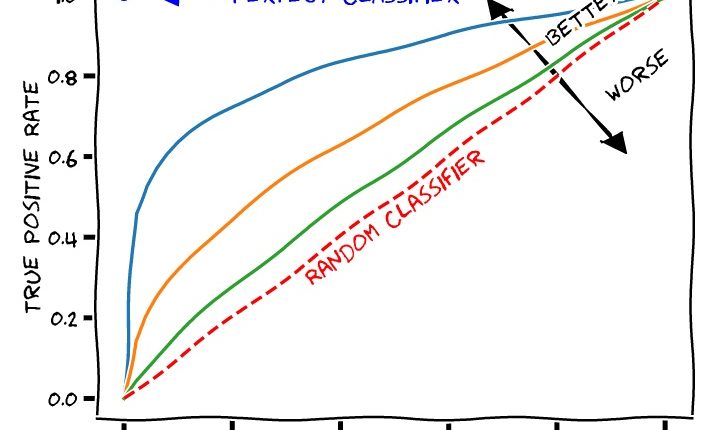
ROC Eğrisi ve AUC Değeri
Üretilmiş modellerin değerlendirmesi makine öğrenmesi üretim hatlarında modellerin sağlamlığının anlaşılabilmesi için önemlidir. Bu noktada da ROC eğrisi ve AUC çok sınıflı sınıflandırma problemlerinin değerlendirme adımında sıkça kullanılan metriklerdir. Bu yazımızda ROC eğrisi ya da Türkçesi ile işlem karakteristik eğrisi, ve AUC yani Türkçesi ile eğri altında kalan alan kavramlarını, model değerlendirme için neden böyle metriklere ihtiyacımız olduğunu, ve python ile nasıl hesaplayabileceğimizi inceleyeceğiz.

Doğruluk metriği çoğunlukla yetersizdir
Fraud işlemlerin tespiti ya da kanser teşhisi gibi vakaları düşünelim. Bütün veri seti içerisinde sadece ufak bir kısım pozitif vaka olarak etiketlenmişken, büyük kısmı negatif olarak etiketlenecektir. Negatif fraud işlemleri %99.9 şeklinde düşünebilirsiniz. Bu durumda bir model bile geliştirmeden girdi setinden bağımsız negatiftir şeklinde bir program yazarsanız başarı oranınız yüksek olacaktır.
|
1 2 3 4 5 6 7 |
def classifier(X): #ignore input X features return False |
Yukarıda yazdığımız programımız bu durumda %99.9 başarı ile cevap dönecektir. Fakat bu yeterli değildir. Burada önemli olan nadir vakaların doğru tespit edilebilmesidir. Bu sebeple sınıflandırma problemlerinde doğruluktan çok precision ve recall metriklerini kullanıyoruz. Türkçeye kesinlik ve hassasiyet olarak çevirebileceğimiz bu metriklerde pozitif olarak tahmin ettiğimiz vakaların gerçekten kaçı pozitif, ve gerçekten pozitif olan vakaların kaçını pozitif olarak tahmin ettiğimizi inceliyoruz.

Hassasiyet de her zaman yeterli olmayabilir
Eğer tahmin ettiğiniz sınıflar pozitif ya da negatif gibi belirginse hassasiyet ve kesinlik değerleri ile modelinizi değerlendirebilirsiniz. Örneğin karar ağaçları size belirgin sınıflara ait tahminler yürütür.
Ama yapay sinir ağları, lojistik veya lineer regresyon gibi algoritmalar size belirgin sınıf yerine bir ondalık bir değer dönerler.
Örnek senaryo
Örnek bir vaka üzerinde kesinlik ve hassasiyetin tek başlarına neden yeterli olmadıklarını incelemeye çalışalım. Aşağıda linkini de bıraktığım veri seti üzerinde çalışacağız. Veri seti ilk kolonunda gerçek değerleri 0 ve 1 olarak, ikinci kolonda da tahminleri [0, 1] aralığında skorlar olarak 100 örneklem için tutmakta.
|
1 2 3 4 5 6 7 |
import pandas as pd #Ref: https://github.com/serengil/tensorflow-101/blob/master/dataset/auc-case-predictions.csv df = pd.read_csv("auc-case-predictions.csv") |

Tahmin skorlarının gerçek tahminlere dönüştürülmesi
Gerçek veriler 0 veya 1 şeklinde belirgin sınıflardı. İlk satırda yer alan 0.22 değerini 0 mı yoksa 1 olarak mı nitelemeliyiz? Bunu yapmanın en kolay yolu bir eşik değeri belirleyip bu eşik değerinin üzerinde olan tahmin skorlarını 1, altında kalanları ise 0 olarak nitelemektir. Çoğunlukla insanın eli bu iki sınıfın ortasında yer alan 0.5 değerini eşik değer olarak atamaya gider.
Bu eşik değer için karmaşa matrisini çıkaralım. Öncelikle gerek duyduğumuz değerlerin ilk değerlerini 0 olarak atıyoruz.
|
1 2 3 4 5 6 |
threshold = 0.5 tp = 0; fp = 0; fn = 0; tn = 0 |
Sonra veri setindeki tüm örneklemlerin üzerinde gezinerek tahmin skorlarının bu eşiğin altında olup olmadıklarını kontrol edeceğiz.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
for index, instance in df.iterrows(): actual = instance["actual"] prediction = instance["prediction"] if prediction >= threshold: prediction_class = 1 else: prediction_class = 0 |
Daha sonra her bir örneklemin gerçekte doğru mu yanlış mı, tahmininin de pozitif mi negatif mi olduğunu kontrol etmemiz gerekiyor.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
if prediction_class == 1 and actual == 1: tp = tp + 1 elif actual == 1 and prediction_class == 0: fn = fn + 1 elif actual == 0 and prediction_class == 1: fp = fp + 1 elif actual == 0 and prediction_class == 0: tn = tn + 1 |
Karmaşa matrisinin tüm elemanlarını hesapladıktan sonra kesinlik ve hassasiyeti hesaplayabileceğiz.
|
1 2 3 4 5 6 |
tpr = tp / (tp + fn) fpr = fp / (tn + fp) |
Belirlediğimiz 0.5 eşik değeri için doğru pozitiflerin oranı 0.74 iken; yanlış pozitiflerin oranı da 0.24 olarak hesaplanmış oldular.
Burada sormamız gereken soru eğer eşik değerini farklı bir değer olarak belirleseydi bu başarı oranları ne olurdu? İşte ROC eğrisi tamamen bunu sorgulamak üzerine kurulmuştur.
Farklı eşik değerleri için sonuçlar
Eşik değerini [0, 1] aralığında farklı değerler olarak değiştirip doğru pozitif ve yanlış pozitiflerin değerlerinin gözlemleyelim.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
import numpy as np roc_point = [] thresholds = list(np.array(list(range(0, 1000+1, 1)))/1000) for threshold in thresholds: #do tpr and fpr calculations in this for loop. #... roc_point.append([tpr, fpr]) |
Daha sonra her bir eşik değeri için doğru pozitif ve yanlış pozitif oranlarını pandas data frame olarak saklamak kolay olacaktır.
|
1 2 3 4 5 6 |
pivot = pd.DataFrame(roc_point, columns = ["x", "y"]) pivot["threshold"] = thresholds |

ROC eğrisi
Y eksenininde doğru pozitif; X eksenininde de yanlış pozitif oranlarının tutulduğu bir scatter grafiği çizmek bize kaba bir ROC eğrisi verecektir.
|
1 2 3 4 5 6 7 8 |
plt.scatter(pivot.y, pivot.x) plt.plot([0, 1]) plt.xlabel('false positive rate') plt.ylabel('true positive rate') |

İkili sınıflandırma problemi üzerinde çalışmıştık ve örneklemler dengeli dağılmışlardı. Bu durumda rastgele bir sayı üreticisinin %50 başarıya sahip olacağını düşünebiliriz. Grafikteki (0,0) noktasından (1, 1) noktasına giden doğru rastgele sayı üreticini temsil etmekte. ROC eğrisinin bunun üzerinde yer almasını bekliyoruz. Mükemmel bir sınıflandırıcımız olsaydı da ters L harfi şeklinde bir grafik ortaya çıkacaktı.
AUC değeri
AUC eğrinin altında kalan alanın kısaltmasıdır. Rastgele sayı üreticisinin bir üçgen oluşturduğunu ve bunun alanının 0.5 olduğunu görüyoruz. Ters L harfi şeklindeki mükemmel sınıflandırıcı da bir kare oluştururdu ve bunun alanı da 1 olurdu. AUC skorunu hesaplamak için bizim eğrimizin altındaki alanı hesaplamamız gerekiyor. Bu da integral va calculus hesaplamaları gerektirmektedir. Ama şanslıyız ki numpy bunu bir fonksiyon haline getirmiştir.
|
1 2 3 4 5 6 |
from numpy import trapz auc = round(abs(np.trapz(pivot.x, pivot.y)), 4) |
AUC skoru bizim eğrimiz için 0.7918 olarak çıkmaktadır. AUC metriği baz alındığında 79.18% oranında başarı hiç de fena görünmüyor.
Sonuç
Bu yazımızda ROC eğrisi ve AUC değerlerine neden ihtiyaç duyduğumuza, ne olduklarına ve nasıl hesaplandıklarının üzerinde durduk. Her ne kadar bir ikili sınıflandırma problemi üzerinde çalışmış olsak da çok sınıflı sınıflandırıcı problemlerini n adet ikili sınıflandırıcı problemine dönüştürebildiğimiz için çok sınıflı sınıflandırıcılar için de AUC değerlerini hesaplayabiliyoruz.
Bu çalışmaya ait kaynak kodunu GitHub’ta paylaştım. Repo’yu yıldızlayarak⭐️ bu çalışmaya katkıda bulunabilirsiniz.
Bu yazıyı A Gentle Introduction to ROC Curve and AUC in Machine Learning yazısından Türkçe’ye çevirdim.